Blog :: What I've Learned About Formal Methods In Half a Year
I started working on my master's degree last September. The goal was to return to my workplace as a domain expert in formal methods – a topic I knew I was interested in, and yet something I knew practically nothing about. I partially attribute my lack of exposure to the lack of supervised learning opportunities (courses) at my undergraduate institution.1 Brown has an ample supply of teaching and research faculty who work in the field, though, so I've been taking advantage of that and soaking up as much knowledge as I can. I'm writing this to summarize what I've learned and done through my few months at grad school, and also to touch on what I have yet to learn because, as it turns out, three semesters is not nearly enough time to become a "domain expert" in anything. A beginning practitioner, perhaps, but I'm sure even that's an overly-generous characterization.2
The two courses I've taken so far which specifically treat formal methods are CSCI 1710: Logic for Systems and CSCI 1951X: Formal Proof and Verification. Shriram Krishnamurti described them, aptly, as two differing approaches to software verification, and I hope that this article gives some intuition as to what those approaches are and how they differ.
I have made an effort to ensure that what I have written here is correct. But, alas, errare humanum est. I am still a student of the topic, and not yet a teacher. You are welcome to contact me or comment below if you find any statements that need to be corrected.
What Are Formal Methods?
It doesn't matter what you call yourself – programmer, software engineer, computer scientist, hobbyist – if you've written software before, you're almost certainly familiar with the idea of testing: writing supplemental code to verify something about some other code you've written. Arguably, the most common form of testing is providing input/output examples. Consider the following program:
(use-modules (srfi srfi-1)
(srfi srfi-26))
(define (singleton? xs) (= 1 (length xs)))
(define (quicksort l)
(if (singleton? l)
l
(append (quicksort (filter (cut > (car l) <>) (cdr l)))
(list (car l))
(quicksort (filter (cut < (car l) <>) (cdr l))))))
We might gain some confidence that this correctly sorts a list by writing a few examples.
(use-modules (srfi srfi-64))
(test-begin "quicksort-test")
(test-equal (quicksort '(1)) '(1))
(test-equal (quicksort '(2 3 1)) '(1 2 3))
(test-end "quicksort-test")
We can also come up with properties that we'd like to be true of the program, and validate it against randomly-generated input instances:3
(define list-max-length 32)
(define (random-list)
(define list-length (+ 1 (random (- list-max-length 1))))
(map (lambda (_) (random 100))
(iota list-length)))
(define (sorted? xs)
(cond ((null? xs) #t)
((singleton? xs) #t)
(else (and (<= (car xs) (cadr xs))
(sorted? (cdr xs))))))
(for-each (lambda (_)
(test-assert (sorted? (quicksort (random-list)))))
(iota 1024))
And, indeed, these sorts of tests are incredibly helpful in writing software, but in practice they will never be exhaustive.4 There is always the possibility that some bug passes by, unbeknownst to your or your team. The "property test" above reveals how insufficient our list of examples is, as the program actually fails on most inputs. But our "property test" has a weakness of its own. In particular, it will claim that everything is okay, even if you replace the sorting algorithm with this:
(define (quicksort l) '(1 2 3))
Of course, this is a contrived example. quicksort is very easy to implement correctly (and, furthermore, to prove correct), but bugs in sorting algorithms that sneak by test suites do come up in practice.
"Formal methods" are those which attempt to address the shortcomings of the typical means of software testing. It's a loaded term. From NASA: formal methods are "mathematically rigorous techniques and tools for the specification, design and verification of software and hardware systems… the specifications used in formal methods are well-formed statements in a mathematical logic and … formal verifications are rigorous deductions in that logic (i.e. each step follows from a rule of inference and hence can be checked by a mechanical process.)"
Our stochastic test to assert the sorted? predicate is a small step in the right direction, as it provides a well-formed specification of one of the properties our program should uphold. But there are other important properties as well – in particular, that the output should be a permutation of the input. For specialized applications of sorting algorithms, we might also care about stability.
The other issue is that we aren't rigorously verifying adherence to our specification. Verifying a few predicates on a few random examples isn't a proof, except in the jocular sense of "proof by example." To really be sure that our code is correct for all possible inputs, we would likely write a proof by (structural) induction and implicitly appeal to the semantics of the programming language we write our program in. If we are fastidious, we can strive prove that these properties hold even as the source code is transformed into machine instructions.
To be more succinct (but far less nuanced), I would say that "formal methods" is the use of mathematical techniques to establish properties about software and verify that those properties hold true. The former part is "formal specification," and the latter is "formal verification."
Why Care?
"Software should be reliable."
The degree to which that statement rings true could depend on your background. In my line of work, a software fault could result in people being sent home in boxes. The software that powers air transportation has to be safe and correct, lest the well-being of any souls on board is at risk. In these cases, policy (law) guides specification (what situations a piece of software needs to be able to handle, and how well), and formal methods are known to help in validating that implementation upholds said specification.
But even if your job doesn't have you losing sleep at night5, that doesn't mean you should care any less about the reliability of your software. It's frustrating to use software that you can't depend on. Have you ever missed an exit because the turn-by-turn navigation software you use has a bug in it? We should strive to write software that doesn't inflict pain or inconvenience upon its users. We should make an effort, when we can, to ensure the software we bring into the world is both minimally harmful and exceptionally useful.
Interest in formal methods in the "non safety-critical" space has been increasing in recent years because downtime, among other things, will reliably lose a company revenue. As an interesting anecdote, the faculty I work with have noted that big cloud providers (Amazon and Microsoft) have been attracting formal methods researchers away from academia with massive salaries because they value reliability and see that formal methods reliably deliver.6
Even if formal methods have a reputation for being costly to adopt, and not reasonably applicable to all parts of the software engineering life cycle, my opinion is that the tooling is becoming increasingly accessible and that software practitioners should, at the very least, be aware of their capabilities. A good engineer knows to pick the right tool for the job, and there are cases where formal methods are just that.
Lightweight Formal Methods: Model and Property Checking
The class I'm taking this semester, CSCI 1710: Logic for Systems, covers model checking with Forge. Forge is practically custom-made for 1710, though it's effectively an alternative implementation of Alloy, which is somewhat better-known. Forge is developed by Tim Nelson alongside a handful of Brown students.
"Lightweight" is a term that's sometimes thrown around when discussing these kinds of model checking tools. I'd summarize lightweight formal methods as those built around the idea that "it's better to have an imperfect tool that's useful than a comprehensive tool that's unusable." Alloy (and, by extension, Forge) is probably the best example of this. It's an attempt at the "smallest modelling notation that can express a useful range of structural properties, is easy to read and write, and can be analyzed automatically".7 It's designed to make it easy to model problems in an abstract and high-level modality.
These tools take, as input, a specification of structural properties in the form of types and predicates, and validate that these expectations about the properties are true. As an example, let's take a homework problem from Operating Systems – another class I'm taking this semester. The problem wasn't particularly difficult, but I think that checking my work with Alloy is a more compelling use-case than any of the toy examples I could come up with.
I'm going to paraphrase the problem text so as to not make the search engine a more useful tool for any future students of the cours.8 The problem pertains to ZFS, which is a copy-on-write file system. All allocated blocks of the file system are organized as one large tree. When an operation is carried out that would modify a disk block, a copy of that block is made and that copy is what gets modified. Said modified copy is linked into the tree by copying the block's parent node and modifying that copy so that it points to the modified block. This continues all the way up to the root, at which point you have two copies of the root: one which represents the filesystem before the operation took place, and one which represents the filesystem after the operation took place. If you keep the old root around, it's a snapshot of the file system before the operation.
The problem asks about when the kernel should free a block that was in the file system. In particular:
- If a file is deleted, how do we know if there's a ZFS snapshot that refers to it?
- If a snapshot is deleted, which files do we free?
Something important to consider when modeling a system with Alloy is whether details are important enough to include, or if they can be omitted for the sake of making the model easier to reason about. For this problem, we aren't concerned with about the tree-like structure of a file system – just the time that files are created, whether or not they're free, and whether or not they're referred to by a snapshot (or the current file system).
(I'm going to use "Alloy" and "Forge" interchangeably in this section, but I am using Forge here.)
An Alloy spec begins with some definitions.
#lang forge
option problem_type temporal
option min_tracelength 2
option max_tracelength 10
sig File {
ctime: one Int,
var free: one Int
}
sig Snapshot extends File {
children: set File,
retired_list: set File
}
one sig CurrentRoot {
var live_children: set File,
var live_retired_list: set File
}
The problem we're dealing with involves a time domain: a file might exist at one point in time, but we might delete it later on. We begin by telling Forge that this is the kind of problem we're dealing with, and that we only care about traces with a number of unique states between 2 and 10.9
We then model the data types in question. You can think of sig like class in Java, or whatever your favorite object-oriented programming language is. In our model, every File has a static ctime representing when the file was created, and whether or not it's free. var means that the field can vary with time, so operations on the filesystem can affect whether or not a file is free, but not the creation time.
This might sound wrong, but it's an intentional modeling choice. Rather than model the file system operations we're concerned with as changing the ctime, we instead treat it as something static, and consider whether or not it's valid only when the file is allocated. In other words: we don't care what the ctime is for a free block, we just care that the ctime is equal to the current time when a file is created.
If that didn't make much sense, it's probably my fault and not yours. That point is a little hard to explain without showing the rest of the code, so just bear with me.
We'll write some predicates next, to model the properties we're interested in.
pred referenced_by_snapshot[f: File] {
some s: Snapshot {
s.free = 0
f in s.children
}
}
pred valid_state {
all f: File {
-- No referenced file should be free.
(f in CurrentRoot.live_children or (some s: Snapshot | f in s.children and s.free = 0)) => f.free = 0
-- No file in a retired list should referenced
f in CurrentRoot.live_retired_list => f not in CurrentRoot.live_children
all s: Snapshot {
f in s.retired_list and s.free = 0 => f not in s.children
}
-- Treat `free` as a boolean.
f.free = 0 or f.free = 1
}
-- Snapshots must be roots.
all s1 : Snapshot {
s1 not in CurrentRoot.live_children
s1 not in CurrentRoot.live_retired_list
all s2: Snapshot {
s1 not in s2.children
s1 not in s2.retired_list
}
}
}
Predicates are sentences in first order logic (albeit with respect to a bounded domain, as we'll explain later). The predicates above should be fairly readable with a light explanation of the syntax. Braces ({}) represent a conjunction, so referenced_by_snapshot is equivalent to
pred referenced_by_snapshot[f: File] | (some s: Snapshot | (s.free = 0 and f in s.children))
"A file f is referenced by a snapshot if there's some snapshot s which isn't free and refers to f by its children relation."
The valid_state is an encoding of the safety properties we care about. We'd like to reason about whether or not our ZFS freeing algorithm ever violates some properties that should be true of our model. In particular, that all files that are "active" in the file system should be allocated, and that the retired list should never refer to an allocated file.
There are some other constraints in the predicate for things which would normally be "obvious," like free being either 0 or 1. An advantage to modeling problems like this in Forge is that it forces you to explicitly enumerate all of your assumptions – if you don't, it will take advantage of that and produce models that might seem nonsensical but are actually completely valid within the constraints you provided. For example, if we didn't have the constraint that f.free = 0 or f.free = 1 for all files, and we asked Forge to generate a model of a valid state, it might build a model where every file has free set to -7. Alloy is really good for forcing you to understand the problem at hand. I'd compare it to having to teach the problem to someone unfamiliar, or explaining a tricky debugging problem to your favorite rubber duck.
Let's define the file system operations now. This is done with predicates as well, which encode whether the post-state accurately reflects a particular operation upon the pre-state.
pred make_snapshot {
one s: Snapshot {
-- The snapshot captures the state of the filesystem at this point in time.
s.children = CurrentRoot.live_children
s.retired_list = CurrentRoot.live_retired_list
-- The snapshot is now marked as allocated.
s.free = 1
s.free' = 0
all f: File {
f != s => {
-- The free flag is unchanged for every other file.
f.free' = f.free
-- All other creations happened in the past, relative to this one.
f.free = 0 => s.ctime > f.ctime
}
}
}
-- The retired list is emptied for the current filesystem.
no live_retired_list'
-- Nothing else changes.
live_children' = live_children
}
pred delete_snapshot {
one s: Snapshot {
-- The snapshot is now marked as free
s.free = 0
s.free' = 1
-- TODO: Add reclaiming operation.
all f: File {
-- The free flag is unchanged for every other file.
f != s => f.free' = f.free
}
}
-- Nothing else changes.
live_retired_list' = live_retired_list
live_children' = live_children
}
pred make_file {
one f: File {
-- `f` is added to the set of live children.
CurrentRoot.live_children' = CurrentRoot.live_children + f
-- `f` is marked as allocated.
f.free' = 0
-- n.b. it could already be allocated, if a previous snapshot refers to it.
all f2: File {
f2 != f => {
-- Free flag for other files remains unchanged.
f2.free' = f2.free
-- All other creations happened in the past, relative to this one.
f2.free = 0 => f.ctime > f2.ctime
}
}
}
-- Nothing else changes.
live_retired_list' = live_retired_list
live_children' = live_children
}
pred delete_file {
one f: File {
-- It only makes sense to delete a file if it's in the filesystem
f in CurrentRoot.live_children
-- Remove it from the filesystem, and reclaim it if applicable.
-- Otherwise, put it in the retired list.
CurrentRoot.live_children' = CurrentRoot.live_children - f
referenced_by_snapshot[f] => {
-- If another snapshot refers to this one, we don't free it
-- but add it to the retired list.
f.free' = 0
CurrentRoot.live_retired_list' = CurrentRoot.live_retired_list + f
} else {
-- Otherwise we can free it and the retired list is unchanged.
f.free' = 1
live_retired_list' = live_retired_list
}
all f2: File {
-- Free flag for other files remains unchanged.
f2 != f => f2.free' = f2.free
}
}
}
Note that I've left a "TODO" in delete_snapshot. We'll add that in later to see how it changes the model.
We should also encode what the file system looks like in the beginning.
-- We start with an empty filesystem, where everything is free.
pred init {
no CurrentRoot.live_children
no CurrentRoot.live_retired_list
all f: File {
f.free = 1 iff f != CurrentRoot
}
}
And with that, we can say what a "trace" looks like.
pred traces {
init
always (make_snapshot or delete_snapshot or make_file or delete_file)
}
We start from nothing and always perform one of the four operations we care about.
With that, we have enough that we can ask Forge some questions. We should make sure that our predicates are satisfiable, and not so over-constrained that they can never be true, and then we should make sure that valid_state is an invariant – that no operation will violate it.
test expect {
valid_state_vacuity1: { valid_state } for 5 File is sat
valid_state_vacuity2: { valid_state } for exactly 5 File is sat
init_vacuity1: { init } for 5 File is sat
init_vacuity2: { init } for exactly 5 File is sat
make_snapshot_vacuity1: { valid_state and make_snapshot } for 5 File is sat
make_snapshot_vacuity2: { valid_state and make_snapshot } for exactly 5 File is sat
make_snapshot_good: {
(valid_state and make_snapshot) => next_state valid_state
} for 5 File is theorem
delete_snapshot_vacuity1: { valid_state and delete_snapshot } for 5 File is sat
delete_snapshot_vacuity2: { valid_state and delete_snapshot } for exactly 5 File is sat
delete_snapshot_good: {
(valid_state and delete_snapshot) => next_state valid_state
} for 5 File is theorem
make_file_vacuity1: { valid_state and make_file } for 5 File is sat
make_file_vacuity2: { valid_state and make_file } for exactly 5 File is sat
make_file_good: {
(valid_state and make_file) => next_state valid_state
} for 5 File is theorem
delete_file_vacuity1: { valid_state and delete_file } for 5 File is sat
delete_file_vacuity2: { valid_state and delete_file } for exactly 5 File is sat
delete_file_good: {
(valid_state and delete_file) => next_state valid_state
} for 5 File is theorem
traces_vacuity: { traces } for 5 File is sat
traces_vacuity: { traces } for exactly 5 File is sat
}
for 5 File tells Forge to consider situations where there are between 0 and 5 files. for exactly 5 File tells Forge to consider situations where there are, well, exactly 5 files. I usually include the latter because some over-constrained predicates are satisfiable precisely when there exactly 0 of something, and I'm usually interested in the case where there is at least 1 of something. The "vacuity" tests are there to ensure that the implication isn't "vacuously" true (i.e., the left-hand side is always false and the implication tells us nothing.)
We can run these tests to find that they all pass. Meaning that if we assume valid_state actually encodes what we mean, our model upholds the invariant. Which is good, because intuition tells us that the implementation where we just leak disk space should be safe.
With that, we can finally answer the second part of the question by updating delete_snapshot to reclaim the free space and see if our invariant is violated.
pred delete_snapshot {
one s: Snapshot {
-- The snapshot is now marked as free
s.free = 0
s.free' = 1
all f: File {
-- Added this
f in s.retired_list => f.free' = 1
-- The free flag is unchanged for every other file.
(f not in s.retired_list and f != s) => f.free' = f.free
}
}
-- Nothing else changes.
live_retired_list' = live_retired_list
live_children' = live_children
}
Let's run it.
jakob@whitecloud ~ $ racket 1670-problem.frg
Forge version: 2.7.0
To report issues with Forge, please visit https://report.forge-fm.org
#vars: (size-variables 1806); #primary: (size-primary 322); #clauses: (size-clauses 3035)
Transl (ms): (time-translation 505); Solving (ms): (time-solving 77)
#vars: (size-variables 1464); #primary: (size-primary 317); #clauses: (size-clauses 2396)
Transl (ms): (time-translation 147); Solving (ms): (time-solving 24)
#vars: (size-variables 1597); #primary: (size-primary 322); #clauses: (size-clauses 2661)
Transl (ms): (time-translation 76); Solving (ms): (time-solving 48)
#vars: (size-variables 1255); #primary: (size-primary 317); #clauses: (size-clauses 2022)
Transl (ms): (time-translation 35); Solving (ms): (time-solving 15)
#vars: (size-variables 3304); #primary: (size-primary 322); #clauses: (size-clauses 8369)
Transl (ms): (time-translation 167); Solving (ms): (time-solving 42)
#vars: (size-variables 2942); #primary: (size-primary 317); #clauses: (size-clauses 7670)
Transl (ms): (time-translation 163); Solving (ms): (time-solving 23)
#vars: (size-variables 38523); #primary: (size-primary 6129); #clauses: (size-clauses 86238)
Transl (ms): (time-translation 1451); Solving (ms): (time-solving 829) Core min (ms): (time-core 0)
#vars: (size-variables 2131); #primary: (size-primary 322); #clauses: (size-clauses 4196)
Transl (ms): (time-translation 64); Solving (ms): (time-solving 21)
#vars: (size-variables 1764); #primary: (size-primary 317); #clauses: (size-clauses 3482)
Transl (ms): (time-translation 54); Solving (ms): (time-solving 21)
#vars: (size-variables 1951); #primary: (size-primary 317); #clauses: (size-clauses 3955)
Transl (ms): (time-translation 52); Solving (ms): (time-solving 17)
Instance found, with statistics and metadata:
(Sat
'(#hash((CurrentRoot . ((CurrentRoot0)))
(File . ((File0) (File1) (File2) (File3) (File4)))
(Snapshot . ((File4)))
(children . ((File4 File2) (File4 File3)))
(ctime . ((File0 5) (File1 -7) (File2 6) (File3 5) (File4 7)))
(free . ((File0 0) (File1 0) (File2 0) (File3 0) (File4 0)))
(live_children . ((CurrentRoot0 File0)))
(live_retired_list . ())
(retired_list . ((File4 File0) (File4 File1))))
#hash((CurrentRoot . ((CurrentRoot0)))
(File . ((File0) (File1) (File2) (File3) (File4)))
(Snapshot . ((File4)))
(children . ((File4 File2) (File4 File3)))
(ctime . ((File0 5) (File1 -7) (File2 6) (File3 5) (File4 7)))
(free . ((File0 1) (File1 1) (File2 0) (File3 0) (File4 1)))
(live_children . ((CurrentRoot0 File0)))
(live_retired_list . ())
(retired_list . ((File4 File0) (File4 File1)))))
'((size-variables 1951)
(size-clauses 3955)
(size-primary 317)
(time-translation 52)
(time-solving 17)
(time-building 1681047504957))
'((prefixLength 2) (loop 1)))
Sterling running. Hit enter to stop service.
Our test fails, and Forge shows us a counterexample! This is the first state:
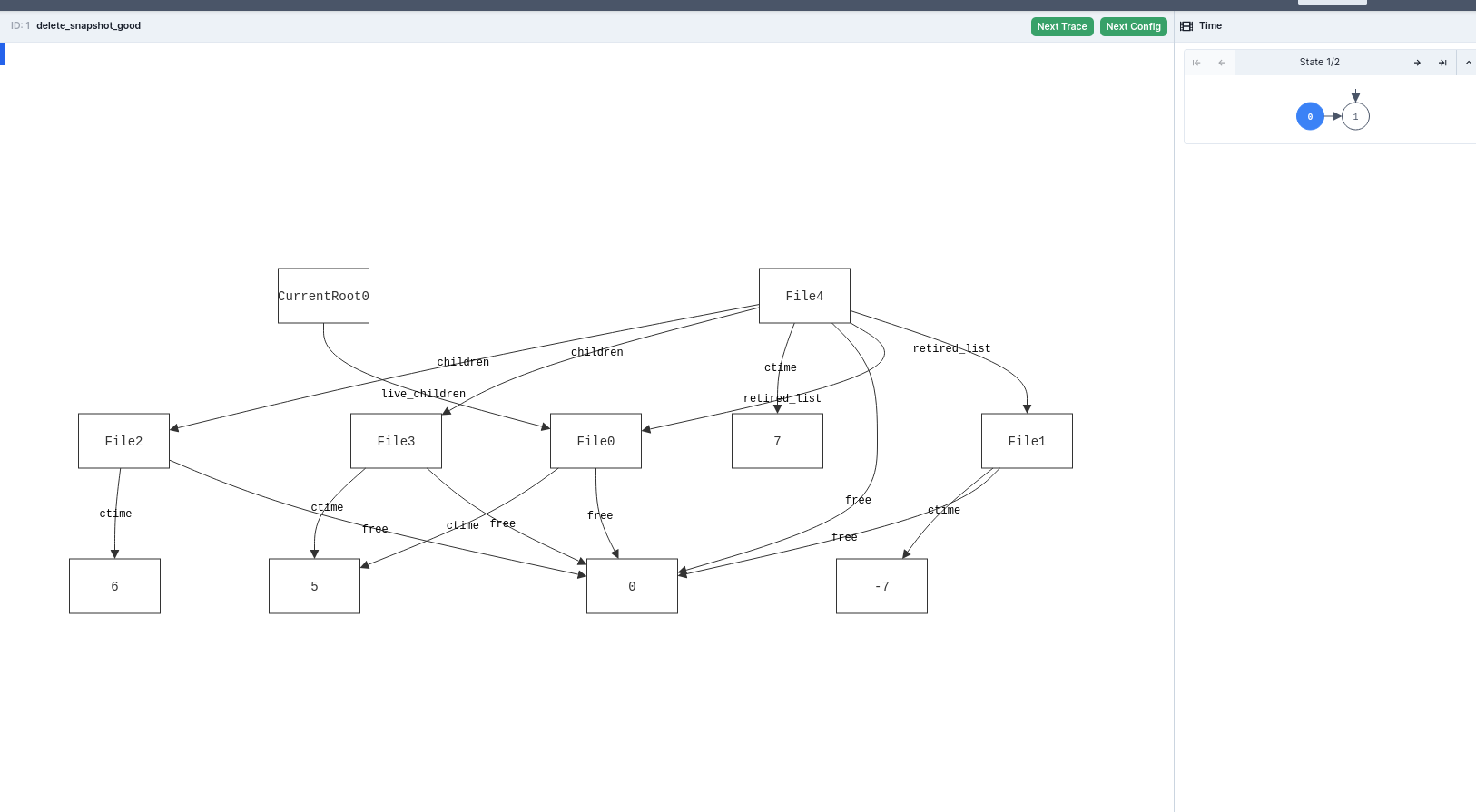
Then we delete a snapshot (File4).
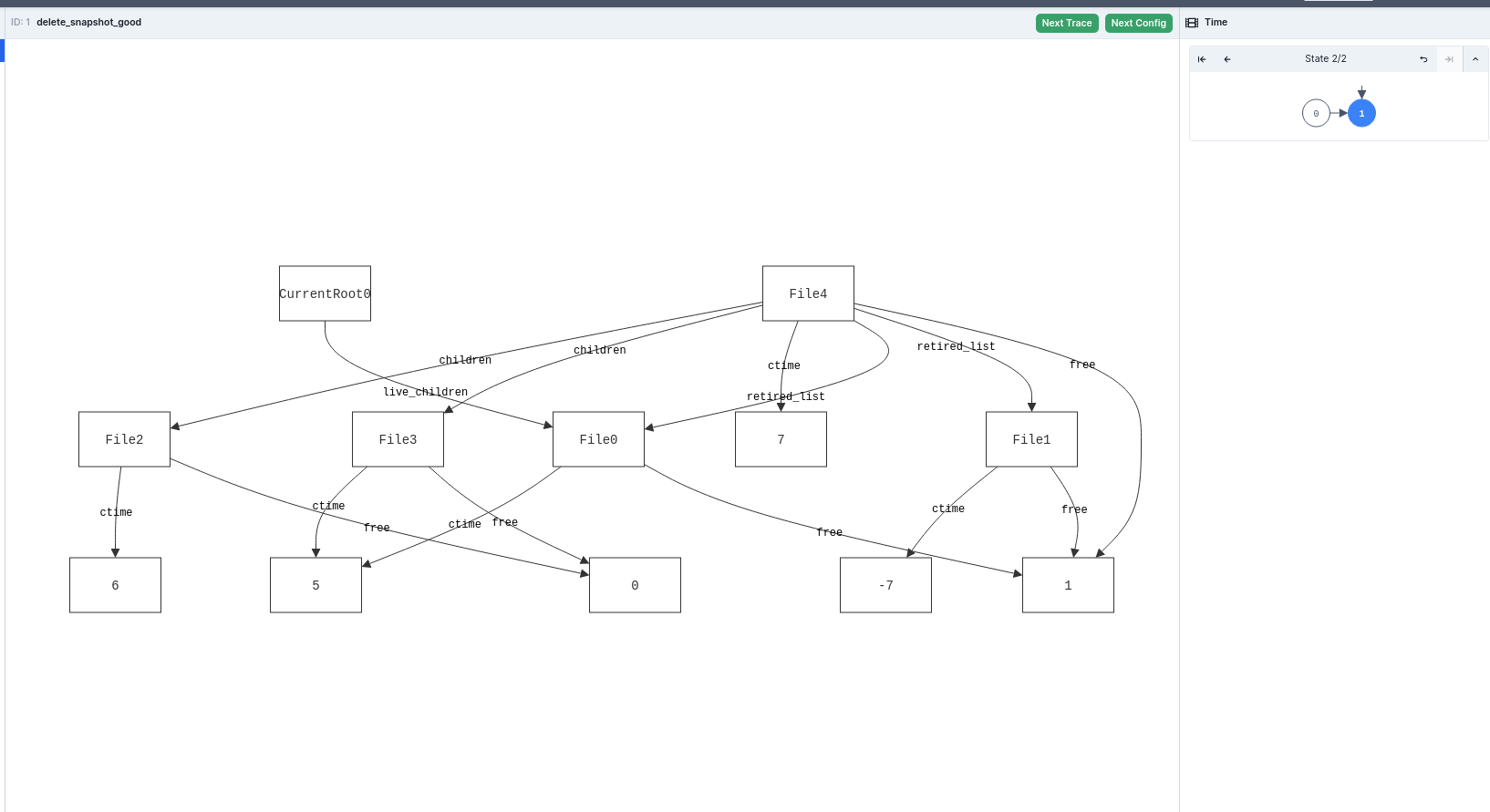
It might be a little hard to visually parse, but File0 is being freed. It's in a snapshot's retired list, but it's live in the current file system as well. So if we free it, we end up violating the invariant that every live file should be allocated.
This is pretty interesting from a counterexample perspective. Can we delete a file and then have it.. come back? Maybe, but I'm going to say "probably not" in the case of this homework problem. (Though it is helpful to have another assumption I can make explicit in my solution set!) So let's treat this as a modeling issue and fix it. The problem is that we have a file that comes back to life: it's in some snapshot's retired_list, but then it also shows back up in the root's live_children. The same issue can also manifest as a file being in a snapshot's retired_list and also in a a later snapshot's children. Let's add this to the safety property:
pred valid_state {
all f: File {
-- No referenced file should be free.
(f in CurrentRoot.live_children or (some s: Snapshot | f in s.children and s.free = 0)) => f.free = 0
-- No file in a retired list should referenced
f in CurrentRoot.live_retired_list => f not in CurrentRoot.live_children
all s: Snapshot {
f in s.retired_list and s.free = 0 => f not in s.children
}
-- Treat `free` as a boolean.
f.free = 0 or f.free = 1
}
-- Snapshots must be roots.
all s1 : Snapshot {
s1 not in CurrentRoot.live_children
s1 not in CurrentRoot.live_retired_list
all s2: Snapshot {
s1 not in s2.children
s1 not in s2.retired_list
}
}
-- Added this!
all f: File | (all s1: Snapshot | f in s1.retired_list => {
f not in CurrentRoot.live_children
all s2: Snapshot {
s2.ctime > s1.ctime => f not in s2.children
}
})
-- This was also necessary -- clock is monotone.
all disj f1, f2: File | f1.ctime != f2.ctime
}
And now we get a more sensible counterexample.
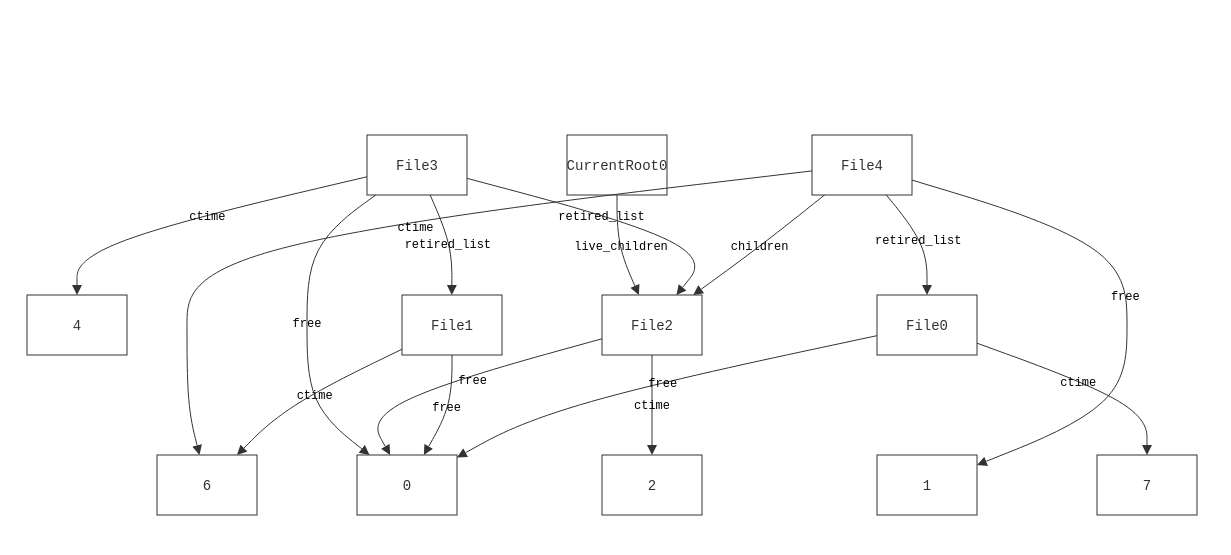
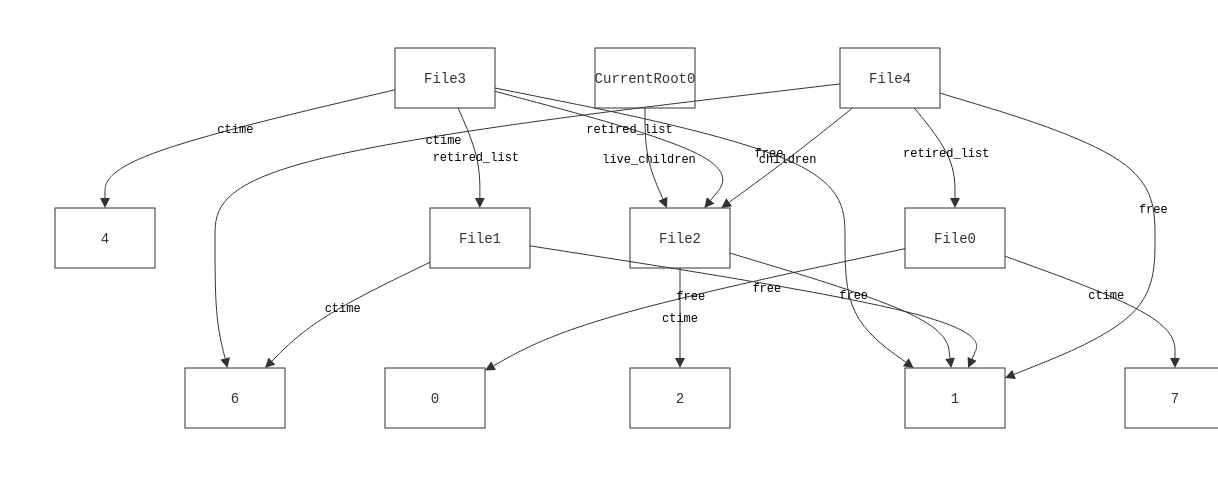
Now we have a file being freed that's also referred to by a previous snapshot. This makes sense, and reveals an actual issue with the approach of "let's delete everything in the retired list." What we actually need to do is check to see if any snapshots refer to an entry in the retired list before deleting it. How we do this is the subject of the first part of the problem, which we'll get to. For now, let's assume we have some efficient predicate to tells us if a file is referenced by an earlier snapshot.
pred referenced_by_no_other_snapshot[f: File] {
all s: Snapshot {
s.free = 0 => f not in s.children
}
}
pred delete_snapshot {
one s: Snapshot {
-- The snapshot is now marked as free
s.free = 0
s.free' = 1
all f: File {
(f in s.retired_list and referenced_by_no_other_snapshot[f]) => {
f.free' = 1
} else {
-- The free flag is unchanged for every other file.
f != s => f.free' = f.free
}
}
}
-- Nothing else changes.
live_retired_list' = live_retired_list
live_children' = live_children
}
jakob@whitecloud ~ $ racket 1670-problem.frg
Forge version: 2.7.0
To report issues with Forge, please visit https://report.forge-fm.org
#vars: (size-variables 3529); #primary: (size-primary 322); #clauses: (size-clauses 7302)
Transl (ms): (time-translation 794); Solving (ms): (time-solving 127)
#vars: (size-variables 3162); #primary: (size-primary 317); #clauses: (size-clauses 6638)
Transl (ms): (time-translation 296); Solving (ms): (time-solving 93)
#vars: (size-variables 1597); #primary: (size-primary 322); #clauses: (size-clauses 2661)
Transl (ms): (time-translation 52); Solving (ms): (time-solving 41)
#vars: (size-variables 1255); #primary: (size-primary 317); #clauses: (size-clauses 2022)
Transl (ms): (time-translation 62); Solving (ms): (time-solving 14)
#vars: (size-variables 3947); #primary: (size-primary 322); #clauses: (size-clauses 9561)
Transl (ms): (time-translation 239); Solving (ms): (time-solving 65)
#vars: (size-variables 3560); #primary: (size-primary 317); #clauses: (size-clauses 8837)
Transl (ms): (time-translation 233); Solving (ms): (time-solving 55)
#vars: (size-variables 44814); #primary: (size-primary 6129); #clauses: (size-clauses 107343)
Transl (ms): (time-translation 2139); Solving (ms): (time-solving 777) Core min (ms): (time-core 0)
#vars: (size-variables 3934); #primary: (size-primary 322); #clauses: (size-clauses 8718)
Transl (ms): (time-translation 126); Solving (ms): (time-solving 48)
#vars: (size-variables 3542); #primary: (size-primary 317); #clauses: (size-clauses 7979)
Transl (ms): (time-translation 121); Solving (ms): (time-solving 31)
#vars: (size-variables 44652); #primary: (size-primary 6129); #clauses: (size-clauses 107046)
Transl (ms): (time-translation 1545); Solving (ms): (time-solving 1413) Core min (ms): (time-core 0)
#vars: (size-variables 3844); #primary: (size-primary 322); #clauses: (size-clauses 9198)
Transl (ms): (time-translation 82); Solving (ms): (time-solving 40)
#vars: (size-variables 3452); #primary: (size-primary 317); #clauses: (size-clauses 8459)
Transl (ms): (time-translation 113); Solving (ms): (time-solving 34)
#vars: (size-variables 43842); #primary: (size-primary 6129); #clauses: (size-clauses 103941)
Transl (ms): (time-translation 1342); Solving (ms): (time-solving 1027) Core min (ms): (time-core 0)
#vars: (size-variables 3831); #primary: (size-primary 322); #clauses: (size-clauses 8652)
Transl (ms): (time-translation 94); Solving (ms): (time-solving 49)
#vars: (size-variables 3454); #primary: (size-primary 317); #clauses: (size-clauses 7958)
Transl (ms): (time-translation 98); Solving (ms): (time-solving 34)
#vars: (size-variables 43761); #primary: (size-primary 6129); #clauses: (size-clauses 105993)
Transl (ms): (time-translation 1218); Solving (ms): (time-solving 1214) Core min (ms): (time-core 0)
#vars: (size-variables 4586); #primary: (size-primary 322); #clauses: (size-clauses 13204)
Transl (ms): (time-translation 111); Solving (ms): (time-solving 34)
#vars: (size-variables 4124); #primary: (size-primary 317); #clauses: (size-clauses 12205)
Transl (ms): (time-translation 80); Solving (ms): (time-solving 10)
#vars: (size-variables 87834); #primary: (size-primary 6273); #clauses: (size-clauses 264636)
Transl (ms): (time-translation 3211); Solving (ms): (time-solving 10304) Core min (ms): (time-core 0)
Sweet. Now, let's tackle the first problem. I posit that this can be determined by walking the snapshots and seeing if any exist with a ctime after the block's ctime and before the time of the deletion.
test expect {
problem_2b: { traces => always {
all f: File | referenced_by_snapshot[f] => {
some s: Snapshot | s.free = 0 and s.ctime > f.ctime
}}} for exactly 5 File is theorem
}
jakob@whitecloud ~ $ racket 1670-problem.frg
Forge version: 2.7.0
To report issues with Forge, please visit https://report.forge-fm.org
#vars: (size-variables 4660); #primary: (size-primary 329); #clauses: (size-clauses 13496)
Transl (ms): (time-translation 910); Solving (ms): (time-solving 67) Core min (ms): (time-core 0)
Nice! Now I have some confidence that my homework answers are right.
What's Going On?
The approach is similar to what we examined before with our stochastic sorting test, except that Forge checks every possible input (up to a bound), rather than sampling a few dozen to check. It's also smart enough to do some pruning, so that the search doesn't take unreasonably long. In a lot of cases, this is sufficient (and far better than the alternative), but if your state space is infinite, the tool won't be able to exhaustively search for a counterexample.
In fact, in 1710, we've often significantly capped the state space. Unless you tell Forge otherwise, integers are 4 bits wide (!), meaning that it only considers every integer as being in $[-8, 7]$. Surprisingly, this is somewhat conducive to discovering bugs, as the effects of integer overflow are more easily observed. Nonetheless, it does mean that a bug that manifests only when a particular integer is, say, $16$, would pass right by you unless you had the insight to increase your bit-width.
How Does It Work?
"Simply" by translating the rules imposed by the model to an instance of SAT/SMT10. If you haven't studied algorithms, SAT is the problem of finding an assignment of values to variables (if one exists) such that a particular boolean formula evaluates to true. A formula, in this case, is a combination of variables joined together by AND, OR, and NOT operators. For example:
$$ a \land b \land \lnot c \lor d $$
A satisfying assignment would be to set $a, b, d$ to "true" and $c$ to "false". SAT is the classical example of an NP-complete problem (though my undergraduate algorithms education focused more on the special case of 3-SAT), but there are still solvers that are reasonably fast, like Z3… which you might be familiar with from some of my earlier writing. There, we used Z3 as a constraint solver: we had some constraints from the key validation algorithm, and had to generate a key that satisfied all of the constraints. The idea here is similar; our abstract specification is translated to a set of constraints (which are encoded as a particular kind of boolean formula), which can then be fed into a SAT/SMT solver.
I've implicitly referred to Z3 as a SAT solver in the preceding paragraph, but it's actually a SMT solver. The difference is that SMT generalizes the satisfiability problem to formulas consisting of more than just booleans. That's why it was useful in our key generation algorithm, since we were dealing with bit vectors and integers and such.
SMT is actually more general than that. SMT stands for "satisfiability modulo theories," and the "modulo theories" part refers to the fact that an SMT instance is interpreted over some set of axioms. A particular set of axioms in Z3 is a "logic," and the reason that Z3 is a "theorem prover" is because it can actually produce proofs of unsatisfiability in certain logic systems… to a point. Often there will be a requirement that the input formula be free of quantifiers. There are nevertheless many interesting theorems which can be formulated (and proved) in light of these restrictions.
At this point in my education, I would like to emphasize the scare quotes in the leading paragraph as much as possible, because I have yet to delve into how that translation actually happens. The SAT/SMT side of formal methods is the one I'm least familiar with, at the time of writing this.
Margrave
As it turns out, model checking is quite useful for access-control policy analysis. An interesting application of model checking is the Margrave Policy Analyzer. The principle underlying the tool is that, although some realizable policies could have an unbounded state space (or one which is too large to exhaustively search), the formulas corresponding to many firewall-analysis problems in practice are amenable to exhaustive analysis. The most compelling feature, in my opinion, is change impact analysis, which I'll briefly introduce by way of analogy: a task I've found Forge to be particularly good at is "diffing" predicates.
test expect {
is_equiv: { prop1 iff prop2 } is theorem
}
Essentially, this checks that prop1 is equivalent to prop2 (if prop1 is true then prop2 is true, and vice versa) and provides a counterexample if that isn't the case. Margrave answers similar questions. Particularly, "if I change or add this rule, what situations are now permitted or denied which would not be so before?" In fact the queries in Margrave are of essentially the same form.
EXPLORE
(InboundACL:Permit(<req>) AND
NOT InboundACL_new:Permit(<req>)) OR
(InboundACL_new:Permit(<req>) AND
NOT InboundACL:Permit(<req>)))
IS POSSIBLE?
The above is "Query 5" from the paper.11 Margrave supports other queries as well, along the same sorts of queries one might make in Alloy. "Show me a run where the principal has these attributes and the decision is to permit, if one exists," or "are there any rules which are superfluous and never apply to any packet?"
Microsoft provides a similar tool using Z3 for analyzing Windows Firewall policies (mostly oriented toward the Azure use-case). This is a nice introductory-level summary.
Formal Specification and Theorem Proving
In my outline, I'd titled this section "heavyweight formal methods: specification and theorem proving," but I'm not sure I've actually heard the term "heavyweight" used to describe these approaches. My intent was to contrast this from the "lightweight" approaches we discussed above. Essentially, we're now considering the opposite end of the spectrum.
My favorite example of "not lightweight" application of formal methods is the seL4 microkernel. It's been around long enough that it's old news by now, but I still think it was (and is) an incredible endeavor. At a high-level, the authors specified some desirable security properties of a microkernel (confidentiality, integrity, and availability) and what interfaces the microkernel should provide in terms of an abstract model. They prove, using Isabelle/HOL, that the interface specification upholds the security properties. Furthermore, they prove that their C implementation refines the abstract model (any behavior observable in the C implementation is a valid behavior in the abstract model), and the verification concludes with a proof that GCC compiles their C implementation correctly.
Theorem Proving
The first thing to understand about the seL4 approach is the class of tooling they leveraged: proof assistants, or theorem provers. NICTA used Isabelle/HOL, which I'm not especially familiar with. The proof assistant I am familiar with is Lean, since it's what Rob Lewis used in his teaching of CSCI 1951X: Formal Proof and Verification, so that's what I'll be writing about.
On the tin, Lean is a theorem prover (or proof assistant), but at its core, it's a dependently-typed functional programming language. What immediately follows from having dependent types and the PAT principle (or Curry-Howard correspondence) is that Lean can be used to reason about logical proofs. I think this is true of Isabelle/HOL, as well as other proof assistants like Coq and Agda.
When you're first learning Lean, it might not be immediately obvious that it's a general-purpose programming language. The first code snippets you'll see are likely to be proofs.
lemma nat.add_comm : ∀ n m : ℕ, n + m = m + n
| n 0 := eq.symm (nat.zero_add n)
| n (m+1) :=
suffices succ (n + m) = succ (m + n), from
eq.symm (succ_add m n) ▸ this,
congr_arg succ (add_comm n m)
This probably does, if you're coming from a programming background, look quite foreign. It may slightly more sensible if you're coming from a math background: this is a lemma about the commutability of addition over the naturals. For two arbitrary natural numbers $n$ and $m$, it is the case that $n + m = m + n$, and the proof proceeds with induction on $m$. Obviously, if $m = 0$, then $n + 0 = 0 + n$. For any other $m$, it suffices to show that $(n + m) + 1 = (m + n) + 1$, which follows from the inductive hypothesis.
But that's an explanation of the underlying math. In the programming language sense, this is code to construct a value of type ∀ n m : ℕ, n + m = m + n – proofs are terms, and propositions are types. If we print out nat.add_comm, we'll see that the result is just a function that takes two natural numbers as inputs.
theorem nat.add_comm : ∀ (n m : ℕ), n + m = m + n :=
λ (n m : ℕ),
nat.brec_on m
(λ (m : ℕ) (_F : nat.below (λ (m : ℕ), ∀ (n : ℕ), n + m = m + n) m) (n : ℕ),
nat.cases_on m
(λ (_F : nat.below (λ (m : ℕ), ∀ (n : ℕ), n + m = m + n) 0),
id_rhs (n + 0 = 0 + n) (eq.symm (nat.zero_add n)))
(λ (m : ℕ) (_F : nat.below (λ (m : ℕ), ∀ (n : ℕ), n + m = m + n) (nat.succ m)),
id_rhs (n + (m + 1) = nat.succ m + n) (eq.symm (nat.succ_add m n) ▸ congr_arg nat.succ (_F.fst.fst n)))
_F)
n
This isn't especially readable, and I doubt Lean practitioners typically inspect proofs in this way, but I think it is instructive to see that the proof boils town to what is effectively a type constructor over two naturals.
Proofs in lean are written either in a forward style:
lemma fst_of_two_props :
∀a b : Prop, a → b → a :=
fix a b : Prop,
assume ha : a,
assume hb : b,
show a, from ha
or in a tactical style:
lemma fst_of_two_props :
∀a b : Prop, a → b → a :=
begin
intros a b,
intros ha hb,
apply ha
end
The former is a sort of forward reasoning, where each line is a step to transform the hypothesis (∀a b : Prop, a → b) into the goal (a), whereas the latter is a sort of backward reasoning, where after eliminating any quantifiers, we're left with the goal and attempt to work backwards. These aren't particularly good examples because they involve only a single step besides quantifier elimination, but I hope they're simple enough to understand.
In the forward-style proof, fix a b is telling Lean that we want to eliminate the ∀ quantifier and say that a, b are two arbitrary propositions. Then we assume the left-most part of a → b → a as ha (a hypothesis that a is true), which leaves us with the task of showing that b → a. Then we assume that b is true, notating this assumption as hb, and then we're left with the task of showing a. Fortunately, this is exactly our assumption ha, so it's easy to show that a is true. Quod erat demonstrandum.
In the tactical style, we're doing the exact same thing, except that we use intros instead of fix or assume. The effect is the same: eliminate some quantifier and give a name to what's being extracted in the environment. In tactic mode, we use apply to transform the "goal state." In this case, our goal is a and we have a hypothesis ha that is exactly a, so we're done when we apply it. But if we had some other hypothesis (say hx) which was b → a, and we did apply hx, our goal state would change to b (to show a, it suffices to show b), and we would still have some work to do. If we still had hb, we could apply hb and then the proof would be complete.
I'll be using tactic mode for the proofs in this article, and I'll make an effort to explain what I'm doing. If you'd like a more detailed tutorial on tactic-mode proofs, I would highly recommend the interactive (browser-based!) Natural Number Game By Kevin Buzzard and Mohammad Pedramfar.
(One other thing I'd like to point out is that some of the examples in this section will be Lean 3 code. The current version of Lean, Lean 4, isn't backwards-compatible with Lean 3. My opinion is that Lean 4 a much better tool, and thus, I'm using it in my research12, but 1951X used Lean 3 and I'd like to be able to present parts my final project without having to rewrite them.)
Compared to SMT, proof assistants tend to be far less restrictive on the kinds of formulas that can be proved. In addition to admitting formulas in higher-order logic, we can also use quantifiers freely in formulating the statements we want to prove. On the other hand, proof assistants have the disadvantage is that there isn't really "push-button automation." There are tools (such as Isabelle's famous sledgehammer) that will automate the proof search, but they're only effective in a handful of cases.
Specification
When we wrote our property tests for Scheme, we formalized our properties as Scheme functions returning booleans (predicates). We did something similar when we wrote our Forge/Alloy predicates as well. I've found that there are (broadly speaking) two approaches to the concept when it comes to proof assistants. One approach is to retain decidability as much as possible and write predicates as boolean returning functions – for example:13
def sorted : List Nat → Bool :=
fun
| (List.nil) => True
| (List.cons x (List.nil)) => True
| (List.cons x₁ (List.cons x₂ xs)) => if x₁ ≤ x₂ then (sorted xs) else False
#eval sorted [1, 2, 3]
-- Lean 4: true
#eval sorted [2, 1, 3]
-- Lean 4: false
If we need to use sorted where a proposition is needed, we can effectively turn it into a Prop by writing sorted ... = True. The other approach is to deal directly with propositions. I've found that in Lean, it's common to encode such predicates inductively.
inductive sorted' : List Nat → Prop
| empty : sorted' (List.nil)
| singleton : sorted' (List.cons x (List.nil))
| tail : (x₁ ≤ x₂) → (sorted' xs) → sorted' (List.cons x₁ (List.cons x₂ xs))
When we define the predicate this way, we lose the ability to request that Lean evaluate it:
#eval sorted' [2, 1, 3]
-- ERROR: failed to synthesize
-- Decidable (sorted' [2, 1, 3])
Which is a bit of a pain, because you sometimes want to be able to complete a proof by saying "well, if we just evaluate this expression, the left-hand side is equal to the right-hand side." So I get the impression it's beneficial to deal with propositions as functions as frequently as possible. I might compare propositions as functions to constructive mathematics, and inductive predicates to classical mathematics.
The examples above are close to what we mean by "predicate" in programming. The first tells you if a list is sorted or not – that fact is either true or false. The second just tells you if a list is sorted, though you can prove that a list is not sorted if no rules can be applied to make the predicate true (by case analysis). In this case, the fact is either true or false as well. But you can have predicates over free variables, or higher-order predicates about the universe. For example, "all lists are sorted" is a predicate that can be represented in Lean as ∀ (xs : List Nat), sorted xs. This is clearly false as we can find a finite counterexample, but higher-order predicates of these form begin to cross the line between decidable and not. We need a proof, rather than a computation, to prove higher-order predicates (though for a finite counterexample, the proof may amount to computation.)
In either case, specification in a theorem prover amounts to writing predicates. I greatly simplified in my above description of the seL4 specification. There is no formal definition of "confidentiality," per se, but some specific properties that arguably fall under the umbrella of confidentiality. For example, that no data cannot be inferred without appropriate read authority.
text \<open>A generalisation of Nonleakage.\<close>
definition Nonleakage_gen :: "bool" where
"Nonleakage_gen \<equiv>
\<forall>as s u t. reachable s \<and> reachable t
\<longrightarrow> s \<sim>schedDomain\<sim> t
\<longrightarrow> s \<approx>(sources as s u)\<approx> t
\<longrightarrow> uwr_equiv s as t as u"
(This is from proof/infoflow/Noninterference_Base.thy.)
Programming Language Semantics
Another way this approach differs from model checking is that we end up dealing with a very low-level specification of the system: its source code. To effectively reason about source code, we need to be able to assign meaning to the different constructs that exist in language, which we can do by providing a formal semantics. There are numerous approaches to doing so, but the three we covered in 1951X were "big-step", "small-step", and "denotational."
Both "big-step" and "small-step" semantics specify rules of inference. In the case of big-step: "if execution of a statement x begins in state S, it will end up in state S'". In the case of small-step: "if execution of a statement x begins in state S, the abstract machine will then end up executing statement x' in state S'." Both represent the same idea, but small-step is much more granular and, hence, is more effective for models of sequential computation akin to the C abstract machine than something like the lambda calculus, so in considering a subset of Scheme for my final project, I gave a "big-step" semantics for said subset. Rules had the following form:
| self_evaluating {expr s}
(h_not_lambda : ¬ is_lambda expr):
big_step
(stmt.expr expr, s)
(expr, s)
Essentially, "for any expr that we can prove isn't a lambda expression there's a 'big step' from the wrapped version of expr to an unwrapped version of expr, and it has no effect on the state." Of course, lambda expressions are self-evaluating in Scheme, but my choice of representation forced me to model that with a separate rule.
| construct_compound_procedure {args body closure s}
(h_well_formed : mk_compound_procedure s args body = except.ok closure):
big_step
(stmt.expr (atom.list ([(atom.symbol "lambda"), args] ++ body)), s)
(closure, s)
I don't feel qualified to give an explanation of denotational semantics. It was explained to me as a way of expressing programming language semantics as "mathematical objects," and we explored that idea by considering programs as relations (particularly the composition of relations), but I suspect there's significant nuance to this because.. I would argue that rules of inference are also mathematical objects. In either case, I'll probably be able to give an explanation in a week or two when I find myself in the deep end. I'll be having to specify programming language semantics very soon as part of what I'm doing with Rob and Shriram.
Refinement
"Refinement" has a very specific meaning in mathematics. In particular, a relation $S^{\prime}$ is said to refine another relation $S$ if $S^{\prime} \subseteq S$. In the case of verifying software, an implementation X "refines" a specification Y if all behaviors that can be observed of X can adequately be explained by the specification Y. More succinctly: the behaviors of X is a subset of the behaviors of Y. There are a lot of different approaches to making refinement tractable but they tend to come down to the idea that we can map states in the abstract model to states in the implementation, and vice versa. This lets us consider the problem of proving that "all programs in the abstract model have a correct equivalent in the concrete model" in pieces rather than as a whole.
This is another area I'm as yet not especially familiar with. I was previously working through Data Refinement: Model-Oriented Proof Methods and their Comparison by de Roever and Engelhardt until I realized that I don't have any near-term need to understand refinement at that level, and decided I would come back to it when it's more apropos.
Application: Proving the Correctness of a Scheme Program
I had originally set out to prove the correctness of the meta-circular evaluator presented in Structure and Interpretation of Computer Programs for my final project, but after finishing my final for cryptography, I had about three restless evenings left to work on the project and I was nowhere near that, so I just submitted an interpreter in Lean and a proof that a program correctly computes the factorial function according to the some semantics for a subset of Scheme.
Most Scheme implementations used today are either R5RS, R6RS, or R7RS, which are far more comprehensive than what my semantics considered. Namely: lambda expressions and evaluations, basic lexical environments, basic control flow, integers and integer arithmetic, symbols, and lists. Notably: no continuations, conditions, strings, or arbitrary-precision arithmetic.
I avoided non-integer numbers because real numbers (shallowly-encoded in Lean) can't really be used in computations (the mathematical definition of a real number encodes an infinite amount of information). Even though the set of integers has infinite cardinality, they're much easier to use and reason about in Lean. Lean 4 has support for floating numbers but, again, we used Lean 3 for this class, so I stuck with Integers.
What follows is a lot of Lean code with minimal commentary. I've had this project tucked away for a couple of months and to explain it like I did the Alloy example would require at least a couple days of refreshing my memory – and I expect the resulting explanation would be incredibly lengthy if I explained everything in as much detail. Don't feel bad about skimming, or skipping to the end entirely. You aren't missing too much if you do. I include this mostly to satisfy any curiosities.
…
Returning to the idea of Lean as a general-purpose programming language… while we can write proofs about the semantics of Lisp without a mechanical parser, I think it's a simple enough example to show off some concepts in Lean. Let's start with a lexical analyzer for s-expressions. Obviously, we'll need some sort of data structure for representing tokens, and Lean fortunately supports inductive (or algebraic, or enumerated) data types.
inductive token : Type
| eof : token
| lparen : token
| rparen : token
| quot : token
| numeral : ℕ → token
| symbol : string → token
They're introduced with inductive. Each name to the left of the : is the constructor (or case) name, and the right-hand side is the type. Like an enum in Rust, inductive data types can contain no information (token) or they can contain some associated data like an integer (ℤ → token) or a string (string → token).
We'll probably also want to be able to print our token streams.
def token.repr : token → string
| (token.eof) := "EOF"
| (token.lparen) := "LPAREN"
| (token.rparen) := "RPAREN"
| (token.quot) := "QUOT"
| (token.numeral n) := "NUMBER " ++ (to_string n)
| (token.symbol s) := "SYMBOL " ++ s
instance : has_repr token := ⟨token.repr⟩
has_repr is like the Show typeclass in Haskell. It specifies an interface for displaying an object as a string. It's a single method in Lean. Here's some pretty awful Lean code for converting a string into a token stream.
meta def take_numeric_helper : list char → list char × list char
| (list.cons x rest) :=
if x.is_digit then
let result := take_numeric_helper rest in
(list.cons x result.fst, result.snd)
else ([], (list.cons x rest))
| _ := ([], [])
meta def take_numeric (s : list char) : (token × list char) :=
let result := take_numeric_helper s in
(token.numeral (string.to_nat (string.join (list.map char.to_string result.fst))),
result.snd)
meta def take_symbol_helper : list char → list char × list char
| (list.cons x rest) :=
if (¬ (x.is_whitespace ∨ x = ')')) then
let result := take_symbol_helper rest in
(list.cons x result.fst, result.snd)
else ([], (list.cons x rest))
| _ := ([], [])
meta def take_symbol (s : list char) : (token × list char) :=
let result := take_symbol_helper s in
(token.symbol (string.join (list.map char.to_string result.fst)),
result.snd)
meta def tokenize_internal : list char → list token
| (list.cons '(' rest) := list.cons token.lparen (tokenize_internal rest)
| (list.cons ')' rest) := list.cons token.rparen (tokenize_internal rest)
| (list.cons '\'' rest) := list.cons token.quot (tokenize_internal rest)
| (list.cons x rest) := if char.is_digit x then
let result := take_numeric (list.cons x rest) in
list.cons result.fst (tokenize_internal result.snd)
else if (¬ char.is_whitespace x) then
let result := take_symbol (list.cons x rest) in
list.cons result.fst (tokenize_internal result.snd)
else
tokenize_internal rest
| _ := [token.eof]
meta def tokenize (s : string) : list token := tokenize_internal (string.to_list s)
#eval tokenize "(define (list-of-values exps env)
(if (no-operands? exps)
'()
(cons (eval (first-operand exps) env)
(list-of-values (rest-operands exps) env))))"
These are all "meta" functions because I don't want to have to prove to Lean that they're well-founded and always terminate. meta functions can be evaluated, but they can't be used in proofs, so they're useful for auxiliary automation and not much else.
Of course, a lexical analyzer is just a step toward building a parser, so we'll model the things we'd like to parse and reason about.
inductive atom : Type
| undefined : atom
| boolean : bool → atom
| number : ℤ → atom
| primitive_procedure : string → atom
| compound_procedure : (string → option atom) → list string → atom → atom
| symbol : string → atom
| list : list atom → atom
| cell : atom → atom → atom
instance atom_inhabited : inhabited atom :=
inhabited.mk (atom.undefined)
The atom type will be useful in specifying the semantics as well as the parser. I'm bastardizing the term somewhat since "atom" has a pretty specific meaning in Lisp that is distinct from how I'm using it here.
inhabited is another typeclass which tells us that an instance of atom can actually be constructed (which isn't true of all types you might want to deal with in Lean.)
We can also write some automation to pretty-print atoms.
meta def atom.repr : atom → string
| (atom.undefined) := "<undefined>"
| (atom.boolean bool) := if bool then "#t" else "#f"
| (atom.number n) := (to_string n)
| (atom.primitive_procedure sym) := "<primitive-procedure: " ++ sym ++ ">"
| (atom.compound_procedure _ args body) := "(λ (" ++ string.intercalate " " args ++ ") " ++ (atom.repr body) ++ ")"
| (atom.symbol sym) := sym
| (atom.list lst) := "(" ++ string.intercalate " " (list.map atom.repr lst) ++ ")"
| (atom.cell car cdr) := "(" ++ atom.repr car ++ " . " ++ atom.repr cdr ++ ")"
meta instance : has_repr atom := ⟨atom.repr⟩
The parser is fairly simple, too, but we have to deal with mutual recursion.
meta def parse_until_rparen : ℤ → list token → option (list token × list token)
| 0 (list.cons (token.rparen) rest) := some ([], rest)
| n (list.cons (token.rparen) rest) :=
match parse_until_rparen (n - 1) rest with
| none := none
| some result := some (list.cons token.rparen result.fst, result.snd)
end
| n (list.cons (token.lparen) rest) :=
match parse_until_rparen (n + 1) rest with
| none := none
| some result := (list.cons token.lparen result.fst, result.snd)
end
| n (list.cons tok rest) :=
match parse_until_rparen n rest with
| none := none
| some result := some (list.cons tok result.fst, result.snd)
end
| n (list.nil) := none
meta mutual def parse_one, parse
with parse_one : list token → option (atom × list token)
| (list.cons token.lparen rest) :=
match parse_until_rparen 0 rest with
| none := none
| some result := some (atom.list (parse result.fst), result.snd)
end
| (list.cons token.quot rest) :=
match parse_one rest with
| none := none
| some result := some (atom.list [(atom.symbol "quote"), result.fst], result.snd)
end
| (list.cons (token.numeral n) rest) := some (atom.number n, rest)
| (list.cons (token.symbol "#t") rest) := some (atom.boolean tt, rest)
| (list.cons (token.symbol "#f") rest) := some (atom.boolean ff, rest)
| (list.cons (token.symbol sym) rest) := some (atom.symbol sym, rest)
| _ := none
with parse : list token → list atom
| (list.nil) := []
| stream := match parse_one stream with
| none := []
| some (result, (list.nil)) := [result]
| some (result, rest) := (list.cons result (parse rest))
end
#eval list.map atom.repr (parse (tokenize "(+ 2 4)"))
#eval list.map atom.repr (parse (tokenize "(define (list-of-values exps env)
(if (no-operands? exps)
'()
(cons (eval (first-operand exps) env)
(list-of-values (rest-operands exps) env))))"))
The evaluator has a notion of errors, whereas the language semantics doesn't, so we'll introduce a type for that as well.
inductive lisp_error : Type
| expected_number : lisp_error
| expected_symbol : lisp_error
| expected_list : lisp_error
| no_such_variable : string → lisp_error
| bad_lambda : lisp_error
| bad_begin : lisp_error
| bad_if : lisp_error
| bad_define : lisp_error
| bad_arity : lisp_error
| excessive_recursion : lisp_error
| unknown_form : lisp_error
def lisp_error.repr : lisp_error → string
| (lisp_error.expected_number) := "Expected number"
| (lisp_error.expected_symbol) := "Expected symbol"
| (lisp_error.expected_list) := "Expected list"
| (lisp_error.no_such_variable sym) := "No such variable: " ++ sym
| (lisp_error.bad_lambda) := "Bad lambda form"
| (lisp_error.bad_begin) := "Bad begin form"
| (lisp_error.bad_if) := "Bad if form"
| (lisp_error.bad_define) := "Bad define form"
| (lisp_error.bad_arity) := "Compound procedure called with wrong number of arguments"
| (lisp_error.excessive_recursion) := "Maximum recursion depth exceeded"
| (lisp_error.unknown_form) := "Unknown form"
instance : has_repr lisp_error := ⟨lisp_error.repr⟩
def lisp_result (α : Type) := except lisp_error α
meta def lisp_result_atom.repr : lisp_result atom → string
| (except.ok result) := atom.repr result
| (except.error err) := "ERROR: " ++ lisp_error.repr err
-- instance : has_repr lisp_result := ⟨lisp_result.repr⟩
meta def lisp_result.repr {α : Type} : lisp_result (atom × α) → string
| (except.ok (result, _)) := atom.repr result
| (except.error err) := "ERROR: " ++ lisp_error.repr err
Now, we also need a notion of "state" and "frame."
def state : Type := string → option atom
instance state_inhabited : inhabited state :=
inhabited.mk (λ x, none)
def state.update (name : string) (val : atom) (s : state) : state :=
λname', if name' = name then some val else s name'
notation s `{` name ` ↦ ` val `}` := state.update name val s
def lookup_var : string → list state → option atom
| var (list.nil) := none
| var (list.cons s rest) :=
match s var with
| some result := some result
| none := lookup_var var rest
end
-- If we've just pushed a frame onto the environment, and a variable exists in
-- that frame, then looking up that variable in the environment is equivalent to
-- looking it up in the frame.
lemma lookup_head (x : string) (y : state) (ys : list state) (z : atom) :
y x = some z → lookup_var x (y :: ys) = some z :=
begin
intro h,
simp [h, lookup_var],
end
def set_var : string → atom → list state → lisp_result (list state)
| place new_value (list.nil) := except.error (lisp_error.no_such_variable place)
| place new_value (list.cons s rest) :=
match s place with
| (some _) := except.ok (list.cons (s{place ↦ new_value}) rest)
| none :=
match set_var place new_value rest with
| (except.ok rest') := except.ok (list.cons s rest')
| (except.error e) := except.error e
end
end
-- This is only well-defined if |names| = |values|.
def new_frame : list string → list atom → state
| (list.cons name rest₁) (list.cons value rest₂) := (new_frame rest₁ rest₂){name ↦ value}
| _ _ := λ _, none
And, finally, we can get into the implementation of evaluation. First, we'll implement evaluation of procedures. Either the procedure is primitive (or built-in), like +, it's a named compound procedure, it's a lambda form, or the name doesn't exist in the environment.
def collect_params : atom → option (list string)
| (atom.list (list.cons (atom.symbol param) rest)) :=
match collect_params (atom.list rest) with
| some rest' := some (list.cons param rest')
| none := none
end
| (atom.list (list.nil)) := some []
| _ := none
#eval collect_params (atom.list [atom.symbol "x"])
#eval collect_params (atom.list [atom.symbol "x", atom.symbol "y"])
def mk_compound_procedure
(closure_env : list state)
(paramlist : atom)
(body : list atom)
: lisp_result atom :=
match collect_params paramlist with
| some params :=
except.ok
(atom.compound_procedure
(λ x, lookup_var x closure_env)
params
(atom.list (list.cons (atom.symbol "begin") body)))
| none := except.error (lisp_error.bad_lambda)
end
#eval lisp_result_atom.repr
(mk_compound_procedure
[(λ _, none)]
(atom.list [atom.symbol "x"])
[(atom.symbol "+"), (atom.number 2), (atom.number 4)])
def symbol_name : atom → option string
| (atom.symbol name) := some name
| _ := none
def is_primitive_procedure (name : string) : bool :=
name ∈ ["+", "-", "*", "/", "=", "car", "cdr", "cons", "null?", "eqv?"]
@[simp]
lemma add_is_primitive : is_primitive_procedure "+" := by exact rfl
@[simp]
lemma sub_is_primitive : is_primitive_procedure "-" := by exact rfl
@[simp]
lemma mul_is_primitive : is_primitive_procedure "*" := by exact rfl
@[simp]
lemma div_is_primitive : is_primitive_procedure "/" := by exact rfl
@[simp]
lemma eq_is_primitive : is_primitive_procedure "=" := by exact rfl
@[simp]
lemma car_is_primitive : is_primitive_procedure "car" := by exact rfl
@[simp]
lemma cdr_is_primitive : is_primitive_procedure "cdr" := by exact rfl
@[simp]
lemma cons_is_primitive : is_primitive_procedure "cons" := by exact rfl
@[simp]
lemma null_is_primitive : is_primitive_procedure "null?" := by exact rfl
@[simp]
lemma eqv_is_primitive : is_primitive_procedure "eqv?" := by exact rfl
def fold_maybe_numeric : (ℤ → ℤ → ℤ) → ℤ → list atom → option ℤ
| op nil (list.cons (atom.number n) rest) :=
do {
rest_sum ← fold_maybe_numeric op nil rest,
pure (op n rest_sum) }
| op nil (list.nil) := some nil
| _ _ _ := none
def primitive_add (args : list atom) : lisp_result atom :=
match fold_maybe_numeric (λ x y, x + y) 0 args with
| some result := except.ok (atom.number result)
| none := except.error lisp_error.expected_number
end
def primitive_sub (args : list atom) : lisp_result atom :=
match fold_maybe_numeric (λ x y, x - y) 0 args with
| some result := except.ok (atom.number result)
| none := except.error lisp_error.expected_number
end
def primitive_mul (args : list atom) : lisp_result atom :=
match fold_maybe_numeric (λ x y, x * y) 1 args with
| some result := except.ok (atom.number result)
| none := except.error lisp_error.expected_number
end
def primitive_div (args : list atom) : lisp_result atom :=
match fold_maybe_numeric (λ x y, x / y) 1 args with
| some result := except.ok (atom.number result)
| none := except.error lisp_error.expected_number
end
def attach_state : lisp_result atom → list state → lisp_result (atom × list state)
| (except.ok result) s := except.ok (result, s)
| (except.error e) _ := except.error e
-- TODO: Error reporting could be better.
def primitive_eq (args : list atom) : lisp_result atom :=
match args with
| (list.cons (atom.number x) (list.cons (atom.number y) _)) :=
except.ok (if x = y then atom.boolean tt else atom.boolean ff)
| _ := except.error lisp_error.expected_number
end
-- This is where I got sick of being explicit about the return types.
def primitive_car (args : list atom) : lisp_result atom :=
match args with
| (list.cons (atom.cell car cdr) _) := except.ok car
| (list.cons car cdr) := except.ok car
| _ := except.error lisp_error.expected_list
end
def primitive_cdr (args : list atom) : lisp_result atom :=
match args with
| (list.cons (atom.cell car cdr) _) := except.ok cdr
| (list.cons car cdr) := except.ok (atom.list cdr)
| _ := except.error lisp_error.expected_list
end
def primitive_cons (args : list atom) : lisp_result atom :=
match args with
| (list.cons car (list.cons (atom.list cdr) _)) := except.ok (atom.list (list.cons car cdr))
| (list.cons car (list.cons cdr _)) := except.ok (atom.cell car cdr)
| _ := except.error lisp_error.expected_list
end
def primitive_null (args : list atom) : lisp_result atom :=
match args with
| (list.cons (atom.list (list.nil)) _) := except.ok (atom.boolean tt)
| (list.cons (atom.list _) _) := except.ok (atom.boolean ff)
| _ := except.error lisp_error.expected_list
end
def primitive_eqv (args : list atom) : lisp_result atom :=
match args with
| (list.cons (atom.symbol x) (list.cons (atom.symbol y) _)) := except.ok (if x = y then atom.boolean tt else atom.boolean ff)
| _ := except.error lisp_error.expected_symbol
end
We can't actually encode a "proper" Scheme implementation in Lean because there'a possibility that we write a program that doesn't terminate. If we cap the maximum evaluation depth, though, we can prove that the evaluator is well-founded. This more accurately models the real world, anyway, since computers have a finite amount of memory. So we have an evaluation_state which maintains the current stack_depth, and we'll use that as both a guardrail that allows us to prove that our recursive eval function eventually terminates.
structure evaluation_state :=
(stack_depth : ℕ)
(environment : list state)
(form : atom)
def evaluation_state_measure : psum evaluation_state (psum evaluation_state evaluation_state) → ℕ
| (psum.inl state) := state.stack_depth
| (psum.inr (psum.inl state)) := state.stack_depth
| (psum.inr (psum.inr state)) := state.stack_depth
mutual def eval, apply, eval_param_list
with eval : evaluation_state → lisp_result (atom × list state)
| (evaluation_state.mk 0 _ _) :=
except.error (lisp_error.excessive_recursion)
| (evaluation_state.mk (stack_depth + 1) s (atom.undefined)) :=
except.ok (atom.undefined, s)
| (evaluation_state.mk (stack_depth + 1) s (atom.boolean bool)) :=
except.ok (atom.boolean bool, s)
| (evaluation_state.mk (stack_depth + 1) s (atom.number n)) :=
except.ok (atom.number n, s)
| (evaluation_state.mk (stack_depth + 1) s (atom.cell car cdr)) :=
except.ok (atom.cell car cdr, s)
| (evaluation_state.mk (stack_depth + 1) s (atom.primitive_procedure name)) :=
except.ok (atom.primitive_procedure name, s)
| (evaluation_state.mk (stack_depth + 1) s (atom.compound_procedure closure_env paramlist body)) :=
except.ok (atom.compound_procedure closure_env paramlist body, s)
| (evaluation_state.mk (stack_depth + 1) s (atom.symbol sym)) :=
if sym = "+" then
except.ok (atom.primitive_procedure "+", s)
else if sym = "-" then
except.ok (atom.primitive_procedure "-", s)
else if sym = "*" then
except.ok (atom.primitive_procedure "*", s)
else if sym = "/" then
except.ok (atom.primitive_procedure "/", s)
else if sym = "=" then
except.ok (atom.primitive_procedure "=", s)
else if sym = "car" then
except.ok (atom.primitive_procedure "car", s)
else if sym = "cdr" then
except.ok (atom.primitive_procedure "cdr", s)
else if sym = "cons" then
except.ok (atom.primitive_procedure "cons", s)
else if sym = "null?" then
except.ok (atom.primitive_procedure "null?", s)
else if sym = "eqv?" then
except.ok (atom.primitive_procedure "eqv?", s)
else match (lookup_var sym s) with
| none := except.error (lisp_error.no_such_variable sym)
| some value := except.ok (value, s)
end
| (evaluation_state.mk (stack_depth + 1) s (atom.list (list.cons func rest))) :=
if symbol_name func = some "quote" then
except.ok (list.head rest, s)
else if symbol_name func = some "lambda" then
match mk_compound_procedure s (list.head rest) (list.tail rest) with
| (except.ok lambda) := except.ok (lambda, s)
| (except.error err) := except.error err
end
else if symbol_name func = some "begin" then
match rest with
| (list.cons head (list.nil)) :=
eval (evaluation_state.mk stack_depth s head)
| (list.cons head tail) :=
match eval (evaluation_state.mk stack_depth s head) with
| (except.ok (result, s')) :=
eval (evaluation_state.mk stack_depth s' (atom.list (list.cons (atom.symbol "begin") tail)))
| (except.error e) := (except.error e)
end
| _ := (except.error lisp_error.bad_begin)
end
else if symbol_name func = some "set!" then
match rest with
| (list.cons (atom.symbol place) (list.cons value _)) :=
match set_var place value s with
| (except.ok s') := except.ok (atom.undefined, s')
| (except.error e) := except.error e
end
| _ := except.error lisp_error.bad_arity
end
else if symbol_name func = some "if" then
match rest with
| (list.cons cond (list.cons ite_true (list.nil))) :=
match eval (evaluation_state.mk stack_depth s cond) with
| except.ok ((atom.boolean ff), s') := except.ok (atom.undefined, s')
| except.ok (_, s') :=
match eval (evaluation_state.mk stack_depth s ite_true) with
| except.ok (result, s'') := except.ok (result, s'')
| except.error e := except.error e
end
| except.error e := except.error e
end
| (list.cons cond (list.cons ite_true (list.cons ite_false _))) :=
match eval (evaluation_state.mk stack_depth s cond) with
| except.ok ((atom.boolean ff), s') :=
match eval (evaluation_state.mk stack_depth s ite_false) with
| except.ok (result, s'') := except.ok (result, s'')
| except.error e := except.error e
end
| except.ok (_, s') :=
match eval (evaluation_state.mk stack_depth s ite_true) with
| except.ok (result, s'') := except.ok (result, s'')
| except.error e := except.error e
end
| except.error e := except.error e
end
| _ := except.error lisp_error.bad_if
end
else if symbol_name func = some "define" then
match rest with
-- Function definition.
| (list.cons (atom.list (list.cons (atom.symbol name) args)) body) :=
match mk_compound_procedure s (atom.list args) body with
| (except.ok procedure) := except.ok (atom.undefined, list.cons ((list.head s){name ↦ procedure}) (list.tail s))
| (except.error e) := except.error e
end
| (list.cons (atom.symbol name) body) :=
match eval (evaluation_state.mk stack_depth s (list.head body)) with
| (except.ok (result, _)) := except.ok (atom.undefined, list.cons ((list.head s){name ↦ result}) (list.tail s))
| (except.error e) := except.error e
end
| _ := except.error lisp_error.bad_define
end
else apply (evaluation_state.mk stack_depth s (atom.list (list.cons func rest)))
| _ := except.error lisp_error.unknown_form
with apply : evaluation_state → lisp_result (atom × list state)
| (evaluation_state.mk 0 _ _) :=
except.error (lisp_error.excessive_recursion)
| (evaluation_state.mk (stack_depth + 1) s (atom.list (list.cons func args))) :=
let func' := eval (evaluation_state.mk stack_depth s func),
args_evaluated := eval_param_list (evaluation_state.mk stack_depth s (atom.list args)) in
match func' with
| (except.ok ((atom.primitive_procedure "+"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_add args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "-"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_sub args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "*"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_mul args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "/"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_div args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "="), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_eq args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "car"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_car args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "cdr"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_cdr args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "cons"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_cons args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "null?"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_null args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure "eqv?"), _)) :=
match args_evaluated with
| (except.ok (args', s')) := attach_state (primitive_eqv args') s
| (except.error e) := except.error e
end
| (except.ok ((atom.primitive_procedure name), _)) :=
except.error (lisp_error.no_such_variable name)
| (except.ok ((atom.compound_procedure closure_env paramlist body), s')) :=
match args_evaluated with
| (except.ok (args', s')) :=
let s'' := (list.cons (new_frame paramlist args') (list.cons closure_env s')) in
eval (evaluation_state.mk stack_depth s'' body)
| (except.error e) := except.error e
end
| _ := except.error (lisp_error.unknown_form)
end
| _ := except.error lisp_error.unknown_form
with eval_param_list : evaluation_state → lisp_result (list atom × list state)
| (evaluation_state.mk 0 _ _) :=
except.error (lisp_error.excessive_recursion)
| (evaluation_state.mk stack_depth s (atom.list (list.nil))) :=
except.ok ([], s)
| (evaluation_state.mk (stack_depth + 1) s (atom.list (list.cons elt rest))) :=
match eval (evaluation_state.mk stack_depth s elt) with
| (except.ok (result_head, s')) :=
match eval_param_list (evaluation_state.mk stack_depth s' (atom.list rest)) with
| except.ok (result_rest, s'') := except.ok (list.cons result_head result_rest, s'')
| (except.error e) := except.error e
end
| (except.error e) := except.error e
end
| _ := except.error lisp_error.unknown_form
using_well_founded {rel_tac := λ _ _, `[exact ⟨_, measure_wf evaluation_state_measure⟩]}
I found the evaluation state structure to actually be quite convenient in reasoning about things like whether or not an evaluation is finite.
lemma finite_implies_nonzero_stack_depth
(form result : atom)
(environment environment' : list state)
(stack_depth : ℕ)
(h_finite : ¬ (eval (evaluation_state.mk stack_depth environment form) = except.error (lisp_error.excessive_recursion))) :
stack_depth > 0 :=
begin
by_contra',
apply h_finite,
simp [le_of_eq] at this,
simp [this, eval],
end
The approach I've taken for the program semantics is to compile the expression to a "statement" type, and then reason about the big step semantics of those statements.
At the beginning, I was doing small step semantics, until I realized that it was really hard to reason about a language where everything is an expression without being able to assume hypotheses about the transitive nature of small steps, which Lean didn't like at all. Something about nesting inductive predicates.
inductive stmt : Type
| expr : atom → stmt -- 1, #tt, symbol, ...
| var : string → stmt -- var-name
| seq : stmt → stmt → stmt -- (begin form ... rest)
| assign : string → stmt → stmt -- (set! name expr)
| define : string → stmt → stmt -- (define name expr)
| ite : stmt → stmt → stmt → stmt -- (if cond expr-true expr-false)
| app : stmt → list stmt → stmt -- ((lambda (arg1 ... argn) body) param1 ... paramn)
meta def stmt.repr : stmt → string
| (stmt.expr expr) := "(expr " ++ atom.repr expr ++ ")"
| (stmt.var name) := "(deref " ++ name ++ ")"
| (stmt.seq car cdr) := "(seq " ++ stmt.repr car ++ " " ++ stmt.repr cdr ++ ")"
| (stmt.assign place rhs) := "(assign " ++ place ++ " " ++ stmt.repr rhs ++ ")"
| (stmt.define place rhs) := "(define " ++ place ++ " " ++ stmt.repr rhs ++ ")"
| (stmt.ite cond if_true if_false) := "(if " ++ stmt.repr cond ++ " " ++ stmt.repr if_true ++ " " ++ stmt.repr if_false ++ ")"
| (stmt.app func args) := "(application " ++ stmt.repr func ++ " " ++ string.intercalate " " (list.map stmt.repr args) ++ ")"
instance stmt_inhabited : inhabited stmt :=
inhabited.mk (stmt.expr (atom.undefined))
def is_some {α : Type} : option α → Prop
| (some _) := true
| _ := false
def is_lambda : atom → Prop
| (atom.list (list.cons (atom.symbol "lambda") _)) := true
| _ := false
def seq_from_list_stmt : list stmt → stmt
| (list.nil) := stmt.expr atom.undefined
| (list.cons head (list.nil)) := head
| (list.cons head tail) := stmt.seq head (seq_from_list_stmt tail)
mutual def compile_stmt, compile_stmt_list
with compile_stmt : atom → option stmt
-- Arity 0
| (atom.list (list.cons func (list.nil))) :=
do {
result ← compile_stmt func,
pure (stmt.app result []) }
-- Arity 1
| (atom.list (list.cons func (list.cons rest (list.nil)))) :=
match func with
| (atom.symbol "begin") := compile_stmt rest
| (atom.symbol "quote") := some (stmt.expr rest)
| _ := do {
result₁ ← compile_stmt func,
result₂ ← compile_stmt rest,
pure (stmt.app result₁ [result₂]) }
end
-- Arity 2
| (atom.list (list.cons func (list.cons place (list.cons rhs (list.nil))))) :=
match func with
| (atom.symbol "begin") :=
do {
result₁ ← compile_stmt func,
result₂ ← compile_stmt place,
result₃ ← compile_stmt rhs,
pure (stmt.seq result₂ result₃) }
| (atom.symbol "set!") :=
match place with
| (atom.symbol place) :=
do {
rhs_result ← compile_stmt rhs,
pure (stmt.assign place rhs_result) }
| _ := none
end
-- We'll convert lambda expressions into compound procedures at evaluation
-- time. We don't have scope information at compile time, so we can't
-- construct closed environments.
| (atom.symbol "lambda") := some (stmt.expr (atom.list [func, place, rhs]))
| (atom.symbol "define") :=
match place with
-- Syntax sugar for (define func (lambda (param₁ ...) body))
| (atom.list (list.cons (atom.symbol func_name) params)) :=
some (stmt.expr
(atom.list ([
(atom.symbol "lambda"),
(atom.list params),
(atom.list [(atom.symbol "begin"), rhs])])))
| (atom.symbol place) :=
do {
rhs_result ← compile_stmt rhs,
pure (stmt.define place rhs_result) }
| _ := none
end
| _ := do {
result₁ ← compile_stmt func,
result₂ ← compile_stmt place,
result₃ ← compile_stmt rhs,
pure (stmt.app result₁ [result₂, result₃]) }
end
-- Arity 3
| (atom.list (list.cons func (list.cons rest_head (list.cons rest_tail₁ (list.cons rest_tail₂ (list.nil)))))) :=
match func with
| (atom.symbol "if") :=
do {
result₁ ← compile_stmt rest_head,
result₂ ← compile_stmt rest_tail₁,
result₃ ← compile_stmt rest_tail₂,
pure (stmt.ite result₁ result₂ result₃)}
| (atom.symbol "begin") :=
do {
result₁ ← compile_stmt rest_head,
result₂ ← compile_stmt rest_tail₁,
result₃ ← compile_stmt rest_tail₂,
pure (stmt.seq result₁ (stmt.seq result₂ result₃))}
| _ := do {
result₁ ← compile_stmt func,
result₂ ← compile_stmt rest_head,
result₃ ← compile_stmt rest_tail₁,
result₄ ← compile_stmt rest_tail₂,
pure (stmt.app result₁ [result₂, result₃, result₄])}
end
-- Arity n > 3
| (atom.list (list.cons func (list.cons rest_head (list.cons rest_tail₁ rest_tail₂)))) :=
match func with
| (atom.symbol "begin") :=
do {
result₁ ← compile_stmt rest_head,
result₂ ← compile_stmt rest_tail₁,
result₃ ← compile_stmt_list rest_tail₂,
pure (stmt.seq result₁ (stmt.seq result₂ (seq_from_list_stmt result₃)))}
-- Generalization of `lambda` above.
-- We're duplicating code to make the equation compiler happy.
| (atom.symbol "lambda") := some (stmt.expr (atom.list (list.cons func (list.cons rest_head (list.cons rest_tail₁ rest_tail₂)))))
-- Syntax sugar for (define func (lambda (param₁ ...) body))
-- We're duplicating code to make the equation compiler happy.
| (atom.symbol "define") :=
match rest_head with
| (atom.list (list.cons (atom.symbol func_name) params)) :=
some (stmt.expr
(atom.list ([
(atom.symbol "lambda"),
(atom.list params),
(atom.list ([(atom.symbol "begin")] ++ (list.cons rest_tail₁ rest_tail₂)))])))
| _ := none
end
| _ := do {
result₁ ← compile_stmt func,
result₂ ← compile_stmt_list (list.cons rest_head (list.cons rest_tail₁ rest_tail₂)),
pure (stmt.app result₁ result₂) }
end
| (atom.list (list.nil)) := none
| (atom.symbol sym) :=
if is_primitive_procedure sym then
some (stmt.expr (atom.primitive_procedure sym))
else some (stmt.var sym)
| e := some (stmt.expr e)
with compile_stmt_list : list atom → option (list stmt)
| (list.cons head rest) :=
match compile_stmt head with
| (some result) :=
match (compile_stmt_list rest) with
| some result_rest := some (list.cons result result_rest)
| none := none
end
| none := none
end
| (list.nil) := some []
def unwrap_option {α : Type} [inhabited α] : option α → α
| (some x) := x
| _ := inhabited.default
mutual inductive args_step, big_step
with args_step : list stmt × list state → list atom × list state → Prop
| nil {s} :
args_step
((list.nil), s)
((list.nil), s)
| cons {S T s s' s'' u r}
(hstep : big_step (S, s) (u, s'))
(hrest : args_step (T, s') (r, s'')) :
args_step
(list.cons S T, s)
(list.cons u r, s'')
with big_step : stmt × list state → atom × list state → Prop
-- I'm not especially happy with this particular rule. I don't think it's
-- unsound, but I'm not 100% confident about that. Unfortunately it's necessary
-- if I don't want to completely rework how function bodies are represented.
| drop_frame {expr u s s' f rest}
(heval_in_frame : big_step (expr, s) (u, s'))
(h_has_frame : s = list.cons f rest) :
big_step (expr, s) (u, rest)
| self_evaluating {expr s}
(h_not_lambda : ¬ is_lambda expr):
big_step
(stmt.expr expr, s)
(expr, s)
| construct_compound_procedure {args body closure s}
(h_well_formed : mk_compound_procedure s args body = except.ok closure):
big_step
(stmt.expr (atom.list ([(atom.symbol "lambda"), args] ++ body)), s)
(closure, s)
| var_deref {x u s}
(h_lookup_var : lookup_var x s = some u):
big_step
(stmt.var x, s)
(u, s)
| seq {S S' T s t t' u}
(hS : big_step (S, s) (S', t))
(hT : big_step (T, t) (u, t')) :
big_step
(stmt.seq S T, s)
(u, t')
| assign {x rhs rhs_expr s s' s''}
(h_rhs_eval : big_step (rhs, s) (rhs_expr, s'))
(h_var_exists : set_var x rhs_expr s' = except.ok s'') :
big_step
(stmt.assign x rhs, s)
(atom.undefined, s'')
| define {x rhs rhs_expr s s'}
(h_rhs_eval : big_step (rhs, s) (rhs_expr, s')) :
big_step
(stmt.define x rhs, s)
(atom.undefined, list.cons ((list.head s'){x ↦ rhs_expr}) (list.tail s'))
| ite_true {b S T s s' t u}
(hcond : big_step (b, s) ((atom.boolean tt), s'))
(heval : big_step (S, s') (u, t)) :
big_step
(stmt.ite b S T, s)
(u, t)
| ite_false {b S T s s' t u}
(hcond : big_step (b, s) ((atom.boolean ff), s'))
(heval : big_step (T, s') (u, t)) :
big_step
(stmt.ite b S T, s)
(u, t)
| application {closed func params body body' args args' expr s s' s'' s'''}
(h_func : big_step (func, s) ((atom.compound_procedure closed params body), s'))
(h_args : args_step (args, s') (args', s''))
(h_well_formed : compile_stmt body = some body')
(heval : big_step (body',
(list.cons (new_frame params args')
(list.cons closed s')))
(expr, s'')) :
big_step
(stmt.app func args, s)
(expr, s''')
| application_primitive_add {s s' args args' n}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_add args' = except.ok (atom.number n)):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "+"))
args, s)
(atom.number n, s)
| application_primitive_sub {s s' args args' n}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_sub args' = except.ok (atom.number n)):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "-"))
args, s)
(atom.number n, s)
| application_primitive_mul {s s' args args' n}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_mul args' = except.ok (atom.number n)):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "*"))
args, s)
(atom.number n, s)
| application_primitive_div {s s' args args' n}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_div args' = except.ok (atom.number n)):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "/"))
args, s)
(atom.number n, s)
| application_primitive_eq {s s' args args' b}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_eq args' = except.ok (atom.boolean b)):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "="))
args, s)
(atom.boolean b, s)
| application_primitive_car {s s' args args' u}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_car args' = except.ok u):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "car"))
args, s)
(u, s)
| application_primitive_cdr {s s' args args' u}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_cdr args' = except.ok u):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "cdr"))
args, s)
(u, s)
| application_primitive_cons {s s' args args' u}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_cons args' = except.ok u):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "cons"))
args, s)
(u, s)
| application_primitive_null {s s' args args' u}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_null args' = except.ok u):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "null?"))
args, s)
(u, s)
| application_primitive_eqv {s s' args args' u}
(h_args : args_step (args, s) (args', s'))
(heval: primitive_null args' = except.ok u):
big_step
(stmt.app
(stmt.expr (atom.primitive_procedure "eqv?"))
args, s)
(u, s)
This is the simplest program I could think of to show that the program semantics are at least usable.
lemma var_lookup :
big_step
(stmt.var "x", [(λ x, none){"x" ↦ atom.number 1}])
((atom.number 1), [(λ x, none){"x" ↦ atom.number 1}]) :=
begin
apply big_step.var_deref,
let my_state := [(λ x, none){"x" ↦ atom.number 1}],
apply lookup_head,
simp [state.update],
end
This is a much more involved proof: that the factorial program at the top of this file is "correct," in the sense that it computes `int.factorial`.
As you'll see, my approach to proving this statement involved many obligations, and ended up being very tedious. It's effectively the "intro to algorithms" proof of correctness for factorial, except that we're appealing to the big-step semantics above. By which I mean – we're doing a rather poor job of leveraging the mathematical tools we just spent pages of code developing. Had I more time to work on this assignment, I might have naturally come to one of the refinement-based solutions, but I chose to be stubborn and just press forward.
def nat.factorial : ℕ → ℤ
| 0 := 1
| (n + 1) := (n + 1) * (nat.factorial n)
def int.factorial : ℤ → ℤ
| (int.of_nat n) := nat.factorial n
| (int.neg_succ_of_nat n) := nat.factorial (n + 1)
-- Would be trivial if there wasn't casting.
lemma sub1_cast (n : ℕ) :
primitive_sub [atom.number (↑n + 1), atom.number 1] = except.ok (atom.number ↑n) :=
sorry
-- Would be trivial (unfold `int.factorial`) if there wasn't casting.
lemma primitive_mul_fact (n : ℕ) :
primitive_mul [atom.number (↑n + 1), atom.number (int.factorial ↑n)] = except.ok (atom.number (int.factorial ↑(nat.succ n))) :=
sorry
-- Would be trivial if comparison was decidable.
lemma factorial_program_compile_inner :
(compile_stmt
(atom.list
[atom.symbol "if", atom.list [atom.symbol "=", atom.number 0, atom.symbol "x"], atom.number 1, atom.list
[atom.symbol "*", atom.symbol "x", atom.list
[atom.symbol "factorial", atom.list [atom.symbol "-", atom.symbol "x", atom.number 1]]]])) =
some
(stmt.ite (stmt.app (stmt.expr (atom.primitive_procedure "="))
[stmt.expr (atom.number 0), stmt.var "x"])
(stmt.expr (atom.number 1))
(stmt.app (stmt.expr (atom.primitive_procedure "*"))
[stmt.var "x",
stmt.app (stmt.var "factorial")
[stmt.app (stmt.expr (atom.primitive_procedure "-"))
[stmt.var "x", stmt.expr (atom.number 1)]]])) :=
sorry
-- For convenience -- the `factorial` function definition is pretty unwieldy to
-- be passing around in theorem statements.
def define_factorial (s : list state) : list state :=
list.cons ((λ _, none){"factorial" ↦
(atom.compound_procedure (λ x, none) ["x"]
(atom.list [
(atom.symbol "if"),
(atom.list [(atom.symbol "="), (atom.number 0), (atom.symbol "x")]),
(atom.number 1),
(atom.list [
(atom.symbol "*"),
(atom.symbol "x"),
(atom.list [
(atom.symbol "factorial"),
(atom.list [
(atom.symbol "-"),
(atom.symbol "x"),
(atom.number 1)])])])]))}) s
lemma factorial_program_correct (n : ℕ) (s : list state) (arg : stmt)
(h_eval_to_n : big_step
(arg, define_factorial s)
(atom.number n, define_factorial s)) :
big_step
(stmt.app (stmt.var "factorial") [arg], define_factorial s)
(atom.number (int.factorial n), define_factorial s) :=
begin
let fundef :=
(atom.compound_procedure (λ x, none) ["x"]
(atom.list [
(atom.symbol "if"),
(atom.list [(atom.symbol "="), (atom.number 0), (atom.symbol "x")]),
(atom.number 1),
(atom.list [
(atom.symbol "*"),
(atom.symbol "x"),
(atom.list [
(atom.symbol "factorial"),
(atom.list [
(atom.symbol "-"),
(atom.symbol "x"),
(atom.number 1)])])])])),
have h_lookup_factorial : lookup_var "factorial" (define_factorial s) = some fundef, by
begin
simp [define_factorial],
apply lookup_head,
simp [state.update],
end,
induction' n,
{ apply big_step.application,
{ apply big_step.var_deref,
simp [h_lookup_factorial, fundef],
apply and.intro,
{ refl, },
{ apply and.intro,
{ refl, },
{ refl, }}},
{ apply args_step.cons,
{ apply h_eval_to_n, },
{ apply args_step.nil, }},
{ exact factorial_program_compile_inner, },
{ apply big_step.ite_true,
{ apply big_step.application_primitive_eq,
{ apply args_step.cons,
{ apply big_step.self_evaluating, simp [is_lambda], },
{ apply args_step.cons,
{ apply big_step.var_deref,
simp [new_frame],
apply lookup_head,
simp [state.update], },
{ apply args_step.nil, }}},
{ unfold primitive_eq, simp, }},
{ apply drop_two_frames,
apply big_step.self_evaluating,
simp [is_lambda], }}},
{ apply big_step.application,
{ apply big_step.var_deref,
simp [h_lookup_factorial, fundef],
apply and.intro,
{ refl, },
{ apply and.intro,
{ refl, },
{ refl, }}},
{ apply args_step.cons,
{ apply h_eval_to_n, },
{ apply args_step.nil, }},
{ exact factorial_program_compile_inner, },
{ apply big_step.ite_false,
{ apply big_step.application_primitive_eq,
{ apply args_step.cons,
{ apply big_step.self_evaluating, simp [is_lambda], },
{ apply args_step.cons,
{ apply big_step.var_deref,
simp [new_frame],
apply lookup_head,
simp [state.update], },
{ apply args_step.nil, }}},
{ unfold primitive_eq,
norm_cast, }},
{ apply drop_two_frames,
apply big_step.application_primitive_mul,
{ apply args_step.cons,
{ apply big_step.var_deref,
simp [new_frame, state.update],
apply lookup_head,
simp, },
{ apply args_step.cons,
{ have hsimp : ∀ (arg : stmt) (u : atom) (s : list state),
big_step (arg, new_frame ["x"] [atom.number ↑(nat.succ n)] :: (λ (x : string), none) :: define_factorial s)
(u, new_frame ["x"] [atom.number ↑(nat.succ n)] :: (λ (x : string), none) :: define_factorial s) ↔
big_step (arg, define_factorial (new_frame ["x"] [atom.number ↑(nat.succ n)] :: (λ (x : string), none) :: define_factorial s))
(u, define_factorial (new_frame ["x"] [atom.number ↑(nat.succ n)] :: (λ (x : string), none) :: define_factorial s)),
by sorry, -- Nontrivial but obvious.
rw hsimp,
apply ih,
{ exact h_lookup_factorial, },
{ apply big_step.application_primitive_sub,
{ apply args_step.cons,
{ have hsimp₂ : lookup_var "x"
(define_factorial
(new_frame ["x"] [atom.number ↑(nat.succ n)] :: (λ (x : string), none) :: define_factorial s)) =
lookup_var "x" (new_frame ["x"] [atom.number ↑(nat.succ n)] :: (λ (x : string), none) :: define_factorial s),
by sorry, -- Nontrivial but obvious.
apply big_step.var_deref,
rw hsimp₂,
simp [new_frame, state.update],
apply lookup_head,
simp, },
{ apply args_step.cons,
{ apply big_step.self_evaluating,
simp [is_lambda], },
{ apply args_step.nil, }}},
{ apply sub1_cast, }}},
{ apply args_step.nil, }}},
apply primitive_mul_fact, }}}
end
The sorry keyword lets you pretend to be Pierre de Fermat and say "this should be provable but I don't want to write the proof down." It's helpful in making some progress when you're working towards a deadline, but it completely violates the soundness of Lean's logic.
I'm not sure how enlightening any of this is, but I think it does highlight how much goes into using these sorts of tools for program verification compared to the ease with which we used Alloy to check my answer to a homework problem.
What I Have Yet to Learn
Quite a bit!
I've alluded to a few things in the previous sections. I have much more to learn about the specification of programming language semantics, and how to apply data refinement in practice. I'm also interested in learning TLA+ and SPARK. They seem to meet somewhere in the middle of Alloy and Lean, which I expect to be the right fit for what I do professionally. I want to learn about the mathematics that underpins SMT, and the algorithms that enable fast SAT solving. I want to learn about how Lean works at a low-level, and the different approaches to encoding logic in a proof assistant.
In short, I've barely scratched the surface. I know enough to be dangerous, but I have a ways to go before I'm the "domain expert" I strive to be.
Conclusions
In this article, we've introduced what formal methods are and gained a cursory understanding of the techniques suited to "high-level" verification and "low-level" verification. "Formal methods" refers to the use of mathematical techniques to establish properties about software and verify that those properties hold true – to provide a higher level of confidence to practitioners about the correctness of software than testing alone. Alloy and Forge are well-suited to working with systems at a high-level and leverage SAT solving to verify properties of interest. Lean, Isabelle, and Coq are well-suited to working with systems at a lower level, and work as a mechanization of mathematical logic: a proof in a proof assistant is equivalent to (but typically more formal than) a proof that a mathematician or computer scientist might write on a piece of paper.
Now that I've got that out of my system, it's time to get back to keeping my head down and working on applying what I've learned to something useful. I hope to write about what I'm working on soon, but this blog can be a bit of a distraction, so I'll be taking a short break from writing for now. See you soon!
Appendix: Using the Tools
Lean 3 is packaged in the Gentoo repositories, but Lean 4 is not. I have an ebuild for it in my overlay if you use Gentoo and you'd like to experiment with Lean 4.
lean-mode was great but lean4-mode forces you into using lsp-mode, which I don't like. (I much prefer eglot.) I'm currently using this fork, which isolates the parts which are specific to lsp-mode. Then all I need to do is set /usr/bin/lake serve as the language server for lean4-mode in eglot-server-programs and add
(defvar lean4-goal-buffer (get-buffer-create "*lean4-goal*"))
(defun lean4-update-goal-buffer ()
(when (eq 'lean4-mode major-mode)
(jsonrpc-async-request
(eglot--current-server-or-lose)
:$/lean/plainGoal (eglot--TextDocumentPositionParams)
:success-fn
(lambda (&rest args)
(let ((goals (seq-reduce #'concat (plist-get (car args) :goals) "")))
(save-excursion
(set-buffer lean4-goal-buffer)
(erase-buffer)
(insert goals))
(message goals)))
:error-fn
(lambda (&rest args) (message (format "JSONrpc error %s" args))))))
(defun lean4-update-goal-buffer-wrap ()
(unless (or (window-minibuffer-p) (not (eq major-mode 'lean4-mode)))
(lean4-update-goal-buffer)))
(add-hook 'post-command-hook #'lean4-update-goal-buffer-wrap)
to my init.el and I get a goal buffer similar to the old lean-mode or Proof General.
—
Footnotes:
CS 691M was last offered in 1996. CS 520 purportedly discusses "formal specification methods." If you read over the syllabus, you'll quickly understand that to be an empty claim. Perhaps I could have self-taught as part of an independent study, but the department (at the time) didn't count independent study credits toward your graduation requirements, and I had another offer (with money involved) to do a REU in cryptography, so that's how I spent the limited time I had available to me.
I've allowed myself to move the goalposts: my purpose is now to learn enough to demonstrate that there would be value in sending me back to school to get my Ph.D. and then truly become a domain expert!
It's uncommon to include stochastic tests such as this one in a "test suite". It's desirable to have a test suite that always passes or always fails.
For more realistic examples of property testing in Scheme, see guile-quickcheck.
One thing also worth noting is that being able to sleep at night now doesn't necessarily mean you won't have to work on safety-critical or mission-critical software later on in your career. If you're merely a hobbyist, maybe these points aren't especially convincing to you.
To be clear: this wasn't my motivation to engage with a study of formal methods.
Jackson, D. (2002). Alloy: a lightweight object modelling notation. ACM Transactions on software engineering and methodology (TOSEM), 11(2), 256-290.
Even so, I'm covering only a small part of the problem, so I wouldn't expect this article to be that useful to someone trying to cheese a homework assignment.
In temporal mode, Forge always generates traces of infinite length, but there will be a loop somewhere within it.
Boolean SATisfiability and Satisfiability Modulo Theories, respectively.
Nelson, T., Barratt, C., Dougherty, D. J., Fisler, K., & Krishnamurthi, S. (2010, November). The Margrave Tool for Firewall Analysis. In LISA (Vol. 10, pp. 1-18).
There is some risk involved in using a new tool that doesn't have a reputation of stability, but there has to be a critical mass of folks taking that risk and being at the forefront of using the tool to help it get a good reputation. I'm choosing to take that risk.
Addendum on August 5th, 2024: Burkhardt Renz pointed out in the comments section that this definition is subtly incorrect. Example: sorted [1, 2, 1] evaluates to true. Rather than (sorted xs), it should be (sorted (List.cons x₂ xs)). This is a good example of where formal methods can fail - if your specification is faulty, then the rest falls apart.
Comments (1)
#eval sorted [1, 2, 1] -- true (sic!)
https://jakob.space
Good catch, thanks! Definitely worth a footnote on the fact that FM is useless if your spec is bad.. and this is an example of a bad spec passing under many peoples' radars.
Leave a Comment